Jet Grouting
Hoy he estado visitando una interesante obra en la que estaban realizando jet grouting con una máquina que permite utilizarse en zonas donde el gálibo este limitado (del orden de 2 m).
Aprovechando la visita os indico algunos datos interesantes por si tenéis que realizar una obra con jet grouting.
- Diámetros de las columnas en función del tipo de jet pueden ser del siguiente orden de magnitud
Jet 1: 0,45-0,80 m
Jet 2: 0.60-2.00 m
Jet 3: 1.00-2.50 m
Superjet 2.00-5.00
Los valores inferiores corresponden a terrenos cohesivos compactos y los mayores a terrenos granulares sueltos.
Es interesante la siguiente fotografía en la que la columna de jet grouting se realizó mediante los mismos parámetros de ejecución pero en dos terrenos diferentes. La superior es en un terreno cohesivo y la inferior con un terreno granular.
- Cuando estudiemos la cantidad de cemento que queda dentro del terreno tratado, tenéis que prever que la cantidad de cemento inyectado debe ser superior a las cantidades efectivas entre 1,8 y 2 veces, dado que durante el proceso de inyección a través de la zona anular dejada por los taladros de perforación, se produce el ascenso hasta la superficie de un caudal del material que resulta de la mezcla del suelo erosionado con una proporción de la lechada inyectada. A este material se le denomina resurgencia o rechazo.La cantidad efectiva de cemento se puede calcular mediante la fórmula de Söding (2009):
Cemento efectivo = 1500 · (γsus–1) · Qsus/(E+Qsus+Qwater),
donde:
γsus – densidad de lechada (a/c)
Qsus – caudal lechada
E – factor de erosión correspondiente al terreno natural
Qwater – caudal de agua (en el caso de precorte)
- Cuando es necesario cambiar el varillaje (y, por tanto, detener el proceso de ejecución del jet) se debe establecer un solape mínimo al inicio de la siguiente maniobra de 20-30 cm.
- Para las características de resistencia y deformabilidad del terreno mejorado, la resistencia a compresión simple del mismo se puede considerar como el parámetro más importante. Así, el valor de la resistencia máxima a tracción del suelo tratado se puede estimar en el orden del 10% de su resistencia a compresión. Y el valor de la resistencia máxima a esfuerzo cortante del suelo tratado se puede estimar en el orden del 8% de su valor de resistencia a compresión
Consolidación secundaria
Estos días estamos viendo en las clases de mecánica del suelo el fenómeno de la consolidación. Para completar lo visto en clase resumo qué se entiende por consolidación secundaria y algunos datos que nos pueden permitir saber si se produce o no este fenómeno.
La consolidación secundaria un asiento adicional debido al reajuste del esqueleto mineral y luego de que la carga está casi toda soportada por el esqueleto del suelo y no por el agua. Aunque en realidad durante este proceso existen pequeñas sobrepresiones intersticiales. Sin embargo, la velocidad del flujo es muy pequeña de manera que las sobrepresiones se pueden considerar inapreciables. Es un fenómeno análogo al de fluencia que presentan materiales sobreconsolidados en el estado plástico.
A continuación comento algunos factores que influyen en la existencia o no de consolidación secundaria:
- Cuanto más tiempo esté aplicada la carga después de la consolidación primaria, mayor será la compacidad obtenida en el terreno.
- La consolidación secundaria es muy importante cuando el incremento de presión aplicada sobre el suelo es pequeñas
- La consolidación secundaria es menos importante si el suelo está sobreconsolidado.
- La consolidación secundaria es más importante cuando son muestras de pequeño espesor. Si se pudiera ensayar una muestra muy delgada la consolidación primaria sería muy corta (se disiparían rápidamente el exceso de presiones intersticiales).
- La consolidación secundaria aumenta al incrementarse el coeficiente de permeabilidad de un suelo ya que el fenómeno de la consolidación primaria se concluiría en menos tiempo.
- La consolidación secundaria es muy importante en suelos con materia orgánica y, especialmente, en la turba.
- También se ha comprobado que el fenómeno es más significativo en aquellos suelos que son muy plásticos.
Ensayo de liberación de tensiones
Para medir las tensiones existentes en un revestimiento de un túnel o en el terreno se pueden hacer ensayos de liberación de tensiones. También se puede estimar la deformabilidad de la roca.
Para realizar el informe, en primer lugar ser colocan, como mínimo, un par de puntos de estudio para poder conocer los movimientos de la fisura. Para ello se debería realizar una fisura en el revestimiento o en la roca.
A continuación se ejecutaría la fisura mediante una sierra o mediante perforación de taladros.
Posteriormente se dejaría que transcurriera cierto tiempo (por ejemplo 24h-36 h). Durante este tiempo se mediría la variación en la apertura de la fisura creada (si está en compresión se cerraría al liberarse las tensiones). Con la medida de los movimientos y conociendo las constantes elásticas de la roca, teóricamente, se puede estimar las tensiones preexistentes. Aunque este cálculo es complejo y se suele tomar como una indicación complementaria (en realidad las tensiones que se miden sólo son las existentes después de la perforación de la ranura).
A continuación se introduce en la fisura practicada un gato y se aplica la presión necesaria hasta que la fisura tenga las mismas dimensiones que inmediatamente después de haberla practicado (se suele emplear un gato plano). Y se estima que la presión necesaria para eliminar la deformación es la presión que existía inicialmente. Evidentemente, el material puede seguir un ciclo de histéresis que haga que las tensiones aplicadas por el gato sean mayores que las preexistentes para llegar a un mismo estado de deformación. El método está especialmente indicado para medir tensiones paralelas a la superficie de una roca y en las proximidades de dicha superficie.
Durante el ensayo además de medir las tensiones es posible medir las deformaciones y, a partir de ese valor, la deformabilidad del macizo rocoso.
A partir del valor de la presión aplicada en el gato para recuperar la deformación producida al realizar el corte es posible determinar la tensión en el terreno/estructura ensayada mediante la siguiente expresión:
σ = p Ka Ke
P: presión comunicada al gato plano
Ke: constante adimensional propia de cada gato plano y del módulo de deformación del material ensayado (la roca o el hormigón del revestimiento). En caso de no disponer de un valor específico de la combinación gato/material se puede tomar un valor igual a la unidad.
Ka: relación entre el área de contacto del gato plano y el área media del corte realizado en la estructura (siempre será inferior a la unidad)
Asiento de un pilote aislado
En muchas ocasiones se suele descir que el asiento del pilote en serivicio es del orden de la centésima parte del diámetro. A continuación vamos a explicar el fndamento de dicha afirmación.
El asiento de un pilote puede estimarse con la siguiente expresión:
s = Np/( 40 Qh) D + L Np / AE
siendo:
Np carga actuante en el pilote
Qh carga de hundimiento
D diámetro del pilote
A área del pilote
E módulo de deformación del hormigón del pilote
L longitud del pilote (en pilotes trabajando por punta, como es el presente caso).
El segundo sumando corresponde al acortamiento elástico del pilote. Considerando una tensión (Np/A) del orden de 35 kp/cm2 y un módulo de deformación de 175.000 kp/cm2, resulta un acortamiento elástico del pilote de:
Selast ≅ 2 X 10-4 · L ≅ 0,2 mm/m · L
Considerando una longitud total de pilote del orden de 10 m, resultaría un valor de Selast ≅ 2 mm.
El primer término corresponde a la deformación del terreno. Teniendo en cuenta que se ha adoptado como criterio Qh/Np > 3, se obtendría:
Sterr = D/120
Teniendo en cuenta, el conjunto de los dos sumandos se llega a las fórmulas simplificadas de uso habitual:
S = D/ 30 F (F = coef. de seguridad = 3)
ó
S =D/100
Esto significa que el orden de magnitud del posible asiento de un pilote de 0,65 m de diámetro es de 6-7 mm.
Por este motivo es muy poco habitual extenderse en consideraciones sobre los asientos cuando se recomiendan pilotes y para ellos se establecen márgenes de seguridad razonables.
Relleno estructural
Antes de comenzar a colocar el relleno estructural será necesario retirar la posible capa de tierra vegetal así como la zona de alteración (un mínimo de 50 cm debe ser siempre retirado).
Para incrementar la eficacia de la compactación será necesario limitar el espesor de tongada una vez compactada. No debería superar los 25 cm. Para ello, evidentemente, se deberá limitar el tamaño máximo de las partículas. El criterio podría ser evitar colocar tamaños superiores a los 8 cm.
La compactación exigida a cada tongada sería tal que la densidad fuera del orden del 97-98% la máxima en el Proctor Modificado (PM). Para realizar el control se debería realizar ensayos Proctor. Además del Proctor se debería conocer su granulometría. Para que el control sea adecuado, es importante comprobar que el Proctor tomado como referencia coincide con el tipo de material que se está empleando en obra. Para ello se podría realizar un ensayo granulométrico diario del material colocado. En muchas ocasiones se considera que el material no está bien compactado cuando en realidad el problema es que el valor de referencia es erróneo.
Además, de establecer como procedimiento de control la densidad, sería bueno establecer un procedimiento de compactación (tipo de compactador, numero de pasadas…) ya que es más sencillo de aplicar en obra.
Para mejorar el comportamiento futuro del relleno sería bueno colocar el material ligeramente del lado húmedo (entre la humedad óptima y la humedad óptima+2%). Este pequeño exceso de humedad facilitaría la puesta en obra (se evitaría arrollarlo durante el paso del rodillo) y reduciría los asientos diferidos. Al tratarse de un material granular este exceso de presión no se convertiría en un exceso de presiones en el material.
Para reducir los asientos postconstructivos se podría colocar una pequeña precarga sobre el relleno (por ejemplo de 1 m de altura). También se podría proceder a regar el relleno una vez construido para disminuir los posibles asientos por humectación futuros. En todo caso, siempre sería bueno que se dejará transcurrir el máximo tiempo posible entre la finalización del relleno y la colocación de la estructura.
Si en algún caso la estructura estuviera próxima al borde del relleno sería recomendable realizar el mismo con un sobreancho de al menos 1 m para así asegurar una adecuada compactación del material. Este sobreancho, evidentemente, debería ser posteriormente retirado.
En todo caso, siempre que se pueda se debería realizar un relleno de prueba para confirmar que los criterios adoptados son correctos.
DEFORMACIÓN NECESARIA PARA MOVILIZAR RESISTENCIA POR PUNTA Y FUSTE EN UN PILOTE
Existe un distinto rango de deformabilidad en los materiales para desarrollar la resitencia por fuste y punta en un pilote. Normalmente, el agotamiento del fuste se produce para deformaciones menores que para la punta. De esta manera, al aplicar la carga vertical en un pilote se puede llegar a “agotar” la resistencia por fuste del pilote y sólo una parte de la resistencia por punta.
Con los modelos numéricos geotécnicos se puede intentar tener en cuenta este efecto, variando la rigidez en el contacto terreno-pilote.
De manera simplificada se puede acudir a algunas referencias. En esta entrada se va a comentar la propuesta realizada por la API. En dicha referencia se indican unas gráficas orientativas en relación con la movilización de la resistencia por fuste y punta en función de la deformación.
Resistencia por fuste
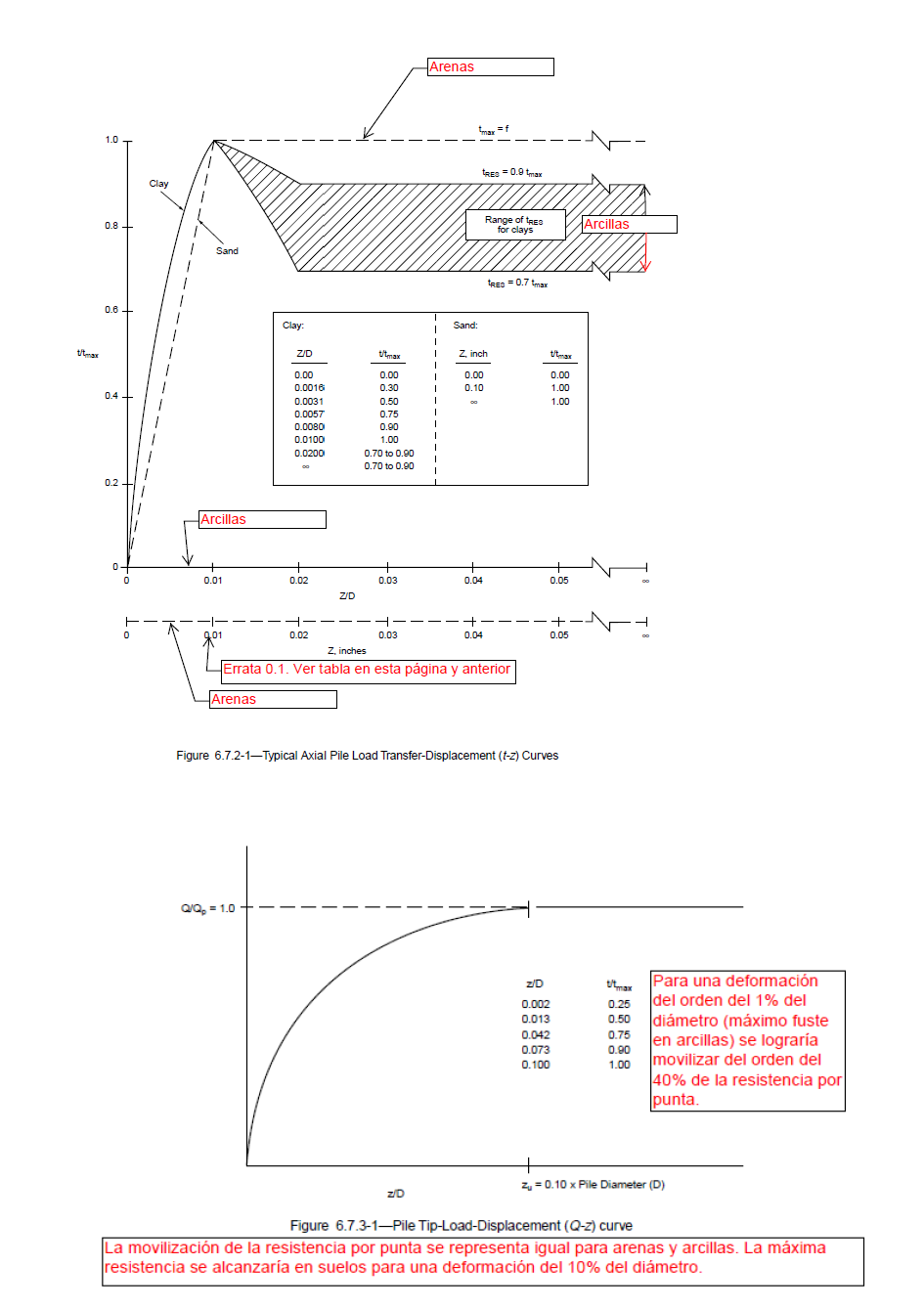
En arenas se alcanza la máxima resistencia por fuste con 0.1 inch (2.54 mm). Si se supera esta deformación, la resistencia por fuste no se reduce para deformaciones mayores.
En arcillas la máxima resistencia por fuste se alcanza para deformaciones del 1% del diámetro. Para deformaciones mayores la resistencia por fuste desciende, situándose en el 70-90% de la máxima
Resistencia por punta
La movilización de la resistencia por punta se representa igual para arenas y arcillas. La máxima resistencia se alcanzaría en suelos para una deformación del 10% del diámetro.
A continuación se muestran los gráficos cargas-deformación de la API tanto para el fuste como para la punta.
Erosión interna de una presa
Hace unos días se produjo la rotura de la balsa de Valverde de la Vera. Según los datos que he podido leer en internet se produjo una pequeña fisura en el cuerpo de la balsa que produjo la posterior rotura. Desde la distancia y sin tener ingún dato objetivo se puede pensar que el fallo esté relacionado con un problema de erosión interna de la balsa (arrastre de material). ¿Se ha producido algún fallo previo en la impermeabilziación que ha dado lugar a este problema de erosión? El objeto de este post no es analizar la rotura producida sino resumir algunas ideas sobre el problema de erosión interna en las presas.
Este problema de erosión interna se ha producido en algunas presas antiguas construidas sin control de filtraciones. En esos casos, puede darse la circunstancia de que el agua aflore en el talud de aguas abajo creando una inestabilidad que, en terrenos granulares, consistiría en deslizamientos superficiales que desorganizarían el talud y podrían conducir a una situación posterior de rotura.
Este problema concreto ha sido objeto de estudio y parece que la situación crítica se alcanza para un cierto caudal crítico, dado por la expresión siguiente:
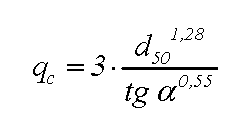
En esta fórmula empírica, propuesta por EBL Kompetanse (2005) el caudal “qc” se expresa en m3/s por m.l. (esto es en m2·s-1) y d50, que es el tamaño medio de las partículas del terreno, se expresa en metros (m). El ángulo α es el que forma el talud de aguas abajo con la horizontal.
Es difícil que una presa construida con un sistema de filtro y dren bien estudiado pueda presentar un problema de erosión interna del propio cuerpo de presa. Pero existen en España algunas presas antiguas construidas sin este sistema esencial de filtro y dren (Cazalegas y Vallehermoso).
Para solventar este tipo de problemas existen, al menos, dos procedimientos posibles:
a) Construir un refuerzo del espaldón de aguas abajo, que incluya un filtro y un dren y sobre ellos un amplio peso, lo que supone tender notablemente el talud de aguas abajo.
b) Construir una pantalla impermeable continua desde el centro de la coronación.
La segunda opción es muy intuitiva pero no resuelve del todo el problema pues sigue faltando un sistema de drenaje que pueda recoger las aguas que se escapen del sistema de impermeabilización. Y por ese motivo, el primer procedimiento parece más adecuado.
Resistencia del bulbo en terrenos cohesivos plásticos (II)
En una entrada anterior llamaba la atención sobre cómo influye la plasticidad de las arcillas en la resistencia límite del bulbo.
Como complemento a aquella entrada muestro el gráfico de Ostermayer, 1974, que se recoge en la British Standard. Además de la consistencia y plasticidad estos diagramas tienen en cuenta el tipo de inyección.
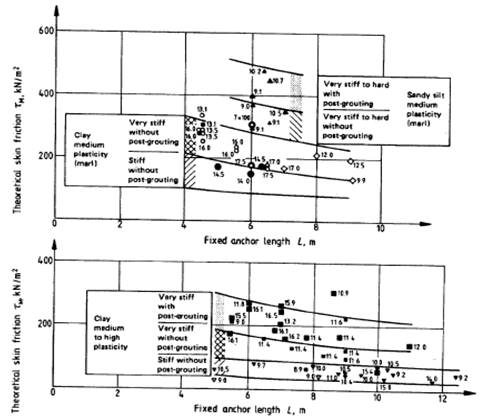
En todo caso es muy importante tener en cuenta que en arcillas plásticas el tema de la inyección es fundamental. Se debería evitar la inyección global única (IGU) en este tipo de materiales. Y siempre que se pueda hacer alguna prueba previa, si es posible, hasta el arrancamiento.
Modulo de deformación en arenas a partir del CPT
En muchas ocasiones tenemos la “necesidad” de obtener los parámetros geotécnicos de manera indirecta a partir de algunos ensayos in situ. En esta entrada se indican algunas expresiones que permiten establecer el módulo de deformación de las arenas a partir del ensayo CPT.
En primer lugar, el método de De Beer y Martins (1957) – De Beer (1965) permite la estimación de asientos en depósitos de arenas estratificadas de arenas de diferente compresibilidad. Asimismo, sugiere la siguiente correlación:
E (kp/cm2) = 1,5 qc
Una modificación al método anterior se debe a Meyerhof (1965) quien propuso que:
E (kp/cm2) = 1,9 qc
En general para arenas, las correlaciones son del siguiente tipo de forma:
Em = a qc
donde: Em es el módulo edométrico.
El coeficiente a varía en el rango de 1,5 a 4 para arenas normalmente consolidadas y de 8 a 15 para arenas sobreconsolidadas. En realidad el factor a depende del grado de consolidación, de la tensión vertical efectiva, de la densidad relativa,… entre otros factores. Vesic (1970) propuso la siguiente expresión dependiente de la densidad relativa:
a = 2 + 2 DR2
Lunne y Christoffersen (1983) propusieron que para niveles granulares se podía emplear la siguiente expresión:
Em= 4 qc si qc < 10 MPa
Em = 2 qc +20 si 10 < qc < 50 MPa
Por último, cabe señalar el trabajo de Schmertmann (1970):
- arenas sumergidas, bien (SW) o mal graduadas (SP)
E (tsf) = 2,5 (qc + 30) ≈E (kp/cm2) = 2,5 (qc + 30)
- arenas sumergidas, mal graduadas (SP) arcillosas:
E (tsf) = 1,67 (qc + 5) ≈ E (kp/cm2) = 1,67 (qc + 5)
Resistencia del bulbo en terrenos cohesivos plásticos
En la “Guía para el diseño y la ejecución de anclajes al terreno en obras de carretera” no se especifican diferentes valores de adherencia para un suelo arcilloso en función de la plasticidad. Sólo es función de la resistencia del suelo. Y esto ha dado lugar, en algunas ocasiones, a sobrevalorar el valor de la adherencia, dando lugar al fallo del anclaje. Así ha sucedido en algunos anclajes realizados en la zona sur de Madrid.
En general, es admitido que cuanto mayor es la plasticidad de las arcillas menor es la adherencia que puede alcanzarse. Pero no existen referencias claras y no es sencillo establecer unos valores fiables. Además, la experiencia indica que las adherencias dependen del procedimiento de inyección, de cómo se realice la perforación e incluso de algunos detalles de la instalación del anclaje.
A continuación, se reproduce una de las pocas referencias en las que el valor de la adherencia del bulbo depende de la plasticidad (aunque sea de manera cualitativa).
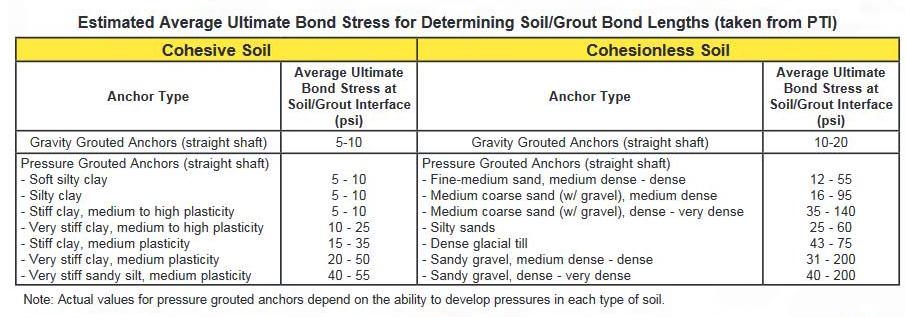
En este tipo de suelos cohesivos plásticos es recomendable realizar inyección repetitiva. Además de poder emplear en el diseño un valor adherencia límite mayor, podremos tener más confianza en dicho valor.
