Inicio » Obras geotécnicas reales (Página 3)
Archivos de la categoría: Obras geotécnicas reales
COEFICIENTE DE BALASTO EN PASOS INFERIORES
Las cargas o tensiones medias transmitidas bajo estos pasos inferiores que corresponden a un marco cerrado son menores que las del terraplén en el que quedan integradas.
Para el cálculo de estas estructuras el único parámetro relevante, a los efectos de realizar el cálculo de la estructura, es el coeficiente de balasto vertical. Realmente este coeficiente, que corresponde a la relación entre la presión y el asiento.
El módulo de balasto, por tanto, no constituye una propiedad geotécnica del terreno, sino que es un artificio de cálculo (que facilita el empleo de los programas de cálculo de estructuras). Por ello, su utilización y los valores asignados al mismo deben tener en cuenta diversos aspectos adicionales (dimensiones del área cargada, estratigrafía del terreno, etc..).
Por otro lado, cuando se estiman los asientos bajo la estructura, no se consideran los inducidos por el incremento de tensiones producido por las tierras adosadas. También hay que tener en cuenta que una parte de los asientos se debe al acortamiento producido en niveles profundos que no producirán asientos diferenciales al nivel de apoyo de la estructura y, por tanto, no inducirán esfuerzos en la losa.
En cualquier caso, este modo de estimar los esfuerzos en la losa inferior está ampliamente difundido en el cálculo de este tipo de estructuras.
El procedimiento empleado para obtener el módulo de balasto se basa en caracterizar los niveles de apoyo suponiendo un modelo elástico lineal (E, módulo de elasticidad y coeficiente de Poisson, ν) y estimar los asientos. Existen diversas fórmulas analíticas para estimar el valor del asiento. Ente otras, la siguiente:
Kv = p/s = (E·b) / [(1-ν2)·(B·L)0,5 ]
donde:
p = presión aplicada
s = asiento de la cimentación
B = ancho de la losa
L = longitud de la losa
b = 1,07 coeficiente de forma para L=B, Davis&Poulos (1973)
E = módulo de elasticidad del terreno
ν = coeficiente de Poisson
Los niveles superficiales del terreno tendrán un módulo relativamente bajo. No obstante, en general, la profundidad de apoyo de la losa es del orden de 1.0-1.5 m, si bien esta profundidad varía en cada caso particular.
Para tener un cierto orden de magnitud del valor del módulo de balasto se supondrá un módulo de deformación de unos 500 kp/cm2. El valor del módulo de Poisson que se considera es de 0.3, el ancho de la losa de 10 m y el espaciamiento entre juntas también de 10 m. Con estos valores resulta el siguiente módulo de balasto:
Kv = p/s = (E·b) / [(1-ν2)·(B·L)0,5 ]= 600 t/m3
El valor de referencia que se supondrá como módulo de balasto para la comprobación de las losas de apoyo de los marcos será de 500 t/m3. Valores de módulos de balasto inferiores al indicado no conllevan un incremento de esfuerzos significativos.
En cada marco se analizaran las condiciones específicas de apoyo y se recomendarán las medidas necesarias para garantizar un apoyo homogéneo sobre un nivel de compacidad media. Para lo cual se propondrán, cuando se considere necesario, sustituciones, recolocaciones, etc. De este modo, se evitan reacciones puntuales y se mejoran las condiciones de apoyo en las zonas donde los niveles superficiales resulten de compacidad baja.
Hundimiento de una placa de carga
La placa de carga es un ensayo que nos permite comprobar el grado de compactación del material. En ocasiones, se han realizado placas de carga en una zona inundada con agua para estudiar el posible colapso del material.
A continuación comparto un caso real que nos va a confirmar cómo las presiones intersticiales producen una disminución de la resistencia.
Durante la carga inicial de un ensayo de placa de carga se evidenciaron síntomas de rotura del terreno: aparecieron grietas cuando se cargó la placa a unas 24 t/m2 y se registró un elevado asiento cuando se alcanzó una carga de unas 35 t/m2. Este ensayo se había realizado con material colocado del lado húmedo.
Sin embargo, anteriormente se había realizado la placa de carga del lado seco sobre el mismo terreno y éste no había colapsado para esas cargas. De hecho, se consiguió cargar la placa hasta 50 t/m2. Esto significaría que la carga de hundimiento debería ser superior a 50 t/m2. De hecho el cálculo teórico mediante la expresión de Brinch Hansen conduciría a un valor de la carga de hundimiento de 120 t/m2.
Ante esta situación cabe preguntarse: ¿por qué se produjo el inicio de la rotura para cargas del orden de 25-35 t/m2 en el ensayo que se hizo del lado húmedo y no ocurrió esto en el ensayo que se hizo seco?
La respuesta a esta pregunta hay que buscarla precisamente en las condiciones de humedad del terraplén. Las determinaciones de humedad que se realizaron in situ antes de la ejecución de la placa de carga mostraron una humedad media del material del orden del 15%. Esto significa que, asumiendo un peso específico del material de 2 t/m3, un volumen de 1m3 de material contiene 2000 kg de terreno y 0.15 · 2000 = 300 litros de agua.
Se trata de un volumen de agua importante. De hecho, para un peso específico de las partículas de valor G = 2.72 t/m3, y para un valor de la densidad seca de γd = 1.85 t/m3, una humedad de valor W = 15% implica un grado de saturación próximo al 90%.
Para humedades de saturación de este orden, lo que ocurre es que al cargar un terreno, el agua que existe en él también se comprime junto con el propio material del terreno, es decir, que se generan presiones intersticiales. Estas presiones intersticiales originan una reducción en la cohesión del terreno, del tal forma que la cohesión de cálculo con la que habría que entrar en la fórmula de Brinch Hansen para considerar la generación de presiones intersticiales sería:
c cálculo =c terreno – u tan Φ
siendo u la presión intersticial que se genera durante el proceso de carga y Φ el ángulo de rozamiento interno del material.
De esta forma, con que se generasen presiones intersticiales de valor medio u = 1.5 t/m2 (situación bastante probable), la cohesión quedaría reducida aproximadamente a la mitad (se pasaría de c = 2t/m2 a c = 1t/m2). Esto explicaría por qué para una carga aplicada de valor inferior a la carga de hundimiento comienzan a aparecer grietas en el terreno y deformaciones elevadas.
Con este caso real sencillo he querido reflejar una vez más la importancia de las presiones intersticiales en el comportamiento del terreno.
Jet Grouting
Hoy he estado visitando una interesante obra en la que estaban realizando jet grouting con una máquina que permite utilizarse en zonas donde el gálibo este limitado (del orden de 2 m).
Aprovechando la visita os indico algunos datos interesantes por si tenéis que realizar una obra con jet grouting.
- Diámetros de las columnas en función del tipo de jet pueden ser del siguiente orden de magnitud
Jet 1: 0,45-0,80 m
Jet 2: 0.60-2.00 m
Jet 3: 1.00-2.50 m
Superjet 2.00-5.00
Los valores inferiores corresponden a terrenos cohesivos compactos y los mayores a terrenos granulares sueltos.
Es interesante la siguiente fotografía en la que la columna de jet grouting se realizó mediante los mismos parámetros de ejecución pero en dos terrenos diferentes. La superior es en un terreno cohesivo y la inferior con un terreno granular.
- Cuando estudiemos la cantidad de cemento que queda dentro del terreno tratado, tenéis que prever que la cantidad de cemento inyectado debe ser superior a las cantidades efectivas entre 1,8 y 2 veces, dado que durante el proceso de inyección a través de la zona anular dejada por los taladros de perforación, se produce el ascenso hasta la superficie de un caudal del material que resulta de la mezcla del suelo erosionado con una proporción de la lechada inyectada. A este material se le denomina resurgencia o rechazo.La cantidad efectiva de cemento se puede calcular mediante la fórmula de Söding (2009):
Cemento efectivo = 1500 · (γsus–1) · Qsus/(E+Qsus+Qwater),
donde:
γsus – densidad de lechada (a/c)
Qsus – caudal lechada
E – factor de erosión correspondiente al terreno natural
Qwater – caudal de agua (en el caso de precorte)
- Cuando es necesario cambiar el varillaje (y, por tanto, detener el proceso de ejecución del jet) se debe establecer un solape mínimo al inicio de la siguiente maniobra de 20-30 cm.
- Para las características de resistencia y deformabilidad del terreno mejorado, la resistencia a compresión simple del mismo se puede considerar como el parámetro más importante. Así, el valor de la resistencia máxima a tracción del suelo tratado se puede estimar en el orden del 10% de su resistencia a compresión. Y el valor de la resistencia máxima a esfuerzo cortante del suelo tratado se puede estimar en el orden del 8% de su valor de resistencia a compresión
Ensayo de liberación de tensiones
Para medir las tensiones existentes en un revestimiento de un túnel o en el terreno se pueden hacer ensayos de liberación de tensiones. También se puede estimar la deformabilidad de la roca.
Para realizar el informe, en primer lugar ser colocan, como mínimo, un par de puntos de estudio para poder conocer los movimientos de la fisura. Para ello se debería realizar una fisura en el revestimiento o en la roca.
A continuación se ejecutaría la fisura mediante una sierra o mediante perforación de taladros.
Posteriormente se dejaría que transcurriera cierto tiempo (por ejemplo 24h-36 h). Durante este tiempo se mediría la variación en la apertura de la fisura creada (si está en compresión se cerraría al liberarse las tensiones). Con la medida de los movimientos y conociendo las constantes elásticas de la roca, teóricamente, se puede estimar las tensiones preexistentes. Aunque este cálculo es complejo y se suele tomar como una indicación complementaria (en realidad las tensiones que se miden sólo son las existentes después de la perforación de la ranura).
A continuación se introduce en la fisura practicada un gato y se aplica la presión necesaria hasta que la fisura tenga las mismas dimensiones que inmediatamente después de haberla practicado (se suele emplear un gato plano). Y se estima que la presión necesaria para eliminar la deformación es la presión que existía inicialmente. Evidentemente, el material puede seguir un ciclo de histéresis que haga que las tensiones aplicadas por el gato sean mayores que las preexistentes para llegar a un mismo estado de deformación. El método está especialmente indicado para medir tensiones paralelas a la superficie de una roca y en las proximidades de dicha superficie.
Durante el ensayo además de medir las tensiones es posible medir las deformaciones y, a partir de ese valor, la deformabilidad del macizo rocoso.
A partir del valor de la presión aplicada en el gato para recuperar la deformación producida al realizar el corte es posible determinar la tensión en el terreno/estructura ensayada mediante la siguiente expresión:
σ = p Ka Ke
P: presión comunicada al gato plano
Ke: constante adimensional propia de cada gato plano y del módulo de deformación del material ensayado (la roca o el hormigón del revestimiento). En caso de no disponer de un valor específico de la combinación gato/material se puede tomar un valor igual a la unidad.
Ka: relación entre el área de contacto del gato plano y el área media del corte realizado en la estructura (siempre será inferior a la unidad)
Asiento de un pilote aislado
En muchas ocasiones se suele descir que el asiento del pilote en serivicio es del orden de la centésima parte del diámetro. A continuación vamos a explicar el fndamento de dicha afirmación.
El asiento de un pilote puede estimarse con la siguiente expresión:
s = Np/( 40 Qh) D + L Np / AE
siendo:
Np carga actuante en el pilote
Qh carga de hundimiento
D diámetro del pilote
A área del pilote
E módulo de deformación del hormigón del pilote
L longitud del pilote (en pilotes trabajando por punta, como es el presente caso).
El segundo sumando corresponde al acortamiento elástico del pilote. Considerando una tensión (Np/A) del orden de 35 kp/cm2 y un módulo de deformación de 175.000 kp/cm2, resulta un acortamiento elástico del pilote de:
Selast ≅ 2 X 10-4 · L ≅ 0,2 mm/m · L
Considerando una longitud total de pilote del orden de 10 m, resultaría un valor de Selast ≅ 2 mm.
El primer término corresponde a la deformación del terreno. Teniendo en cuenta que se ha adoptado como criterio Qh/Np > 3, se obtendría:
Sterr = D/120
Teniendo en cuenta, el conjunto de los dos sumandos se llega a las fórmulas simplificadas de uso habitual:
S = D/ 30 F (F = coef. de seguridad = 3)
ó
S =D/100
Esto significa que el orden de magnitud del posible asiento de un pilote de 0,65 m de diámetro es de 6-7 mm.
Por este motivo es muy poco habitual extenderse en consideraciones sobre los asientos cuando se recomiendan pilotes y para ellos se establecen márgenes de seguridad razonables.
Resistencia del bulbo en terrenos cohesivos plásticos (II)
En una entrada anterior llamaba la atención sobre cómo influye la plasticidad de las arcillas en la resistencia límite del bulbo.
Como complemento a aquella entrada muestro el gráfico de Ostermayer, 1974, que se recoge en la British Standard. Además de la consistencia y plasticidad estos diagramas tienen en cuenta el tipo de inyección.
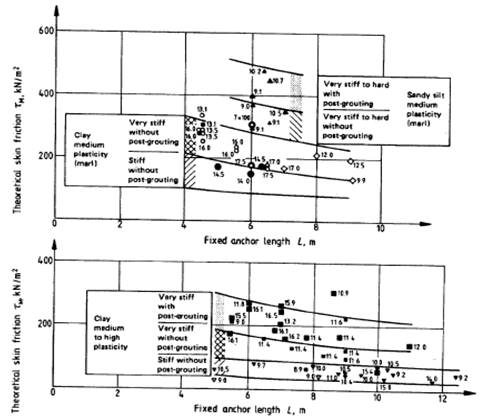
En todo caso es muy importante tener en cuenta que en arcillas plásticas el tema de la inyección es fundamental. Se debería evitar la inyección global única (IGU) en este tipo de materiales. Y siempre que se pueda hacer alguna prueba previa, si es posible, hasta el arrancamiento.
Resistencia del bulbo en terrenos cohesivos plásticos
En la “Guía para el diseño y la ejecución de anclajes al terreno en obras de carretera” no se especifican diferentes valores de adherencia para un suelo arcilloso en función de la plasticidad. Sólo es función de la resistencia del suelo. Y esto ha dado lugar, en algunas ocasiones, a sobrevalorar el valor de la adherencia, dando lugar al fallo del anclaje. Así ha sucedido en algunos anclajes realizados en la zona sur de Madrid.
En general, es admitido que cuanto mayor es la plasticidad de las arcillas menor es la adherencia que puede alcanzarse. Pero no existen referencias claras y no es sencillo establecer unos valores fiables. Además, la experiencia indica que las adherencias dependen del procedimiento de inyección, de cómo se realice la perforación e incluso de algunos detalles de la instalación del anclaje.
A continuación, se reproduce una de las pocas referencias en las que el valor de la adherencia del bulbo depende de la plasticidad (aunque sea de manera cualitativa).
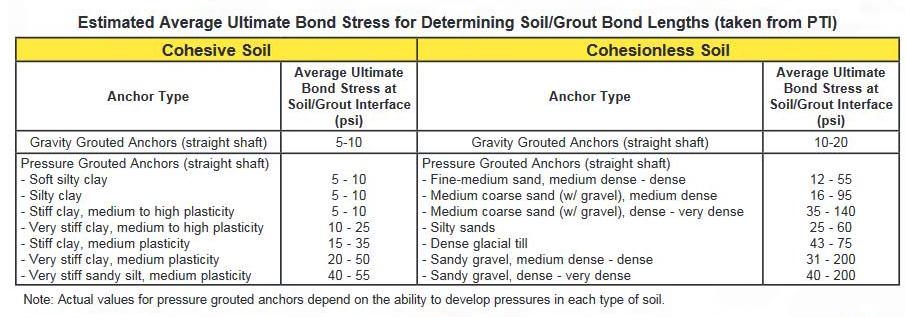
En este tipo de suelos cohesivos plásticos es recomendable realizar inyección repetitiva. Además de poder emplear en el diseño un valor adherencia límite mayor, podremos tener más confianza en dicho valor.
Diámetro “real” del bulbo
Es conocido que cuando calculamos la resistencia del bulbo de un anclaje podemos considerar un diámetro superior al nominal, cuyo valor depende de la naturaleza y compacidad del suelo y del tipo de inyección .
En esta entrada se incluyen las propuestas realizadas por dos auotres a partir de los resultados de ensayos realizados in situ. En primer lugar se muestra el trabajo de Bustamante en el que l valor de α indicado es el cociente entre el diámetro real del bulbo y el diámetro nominal.
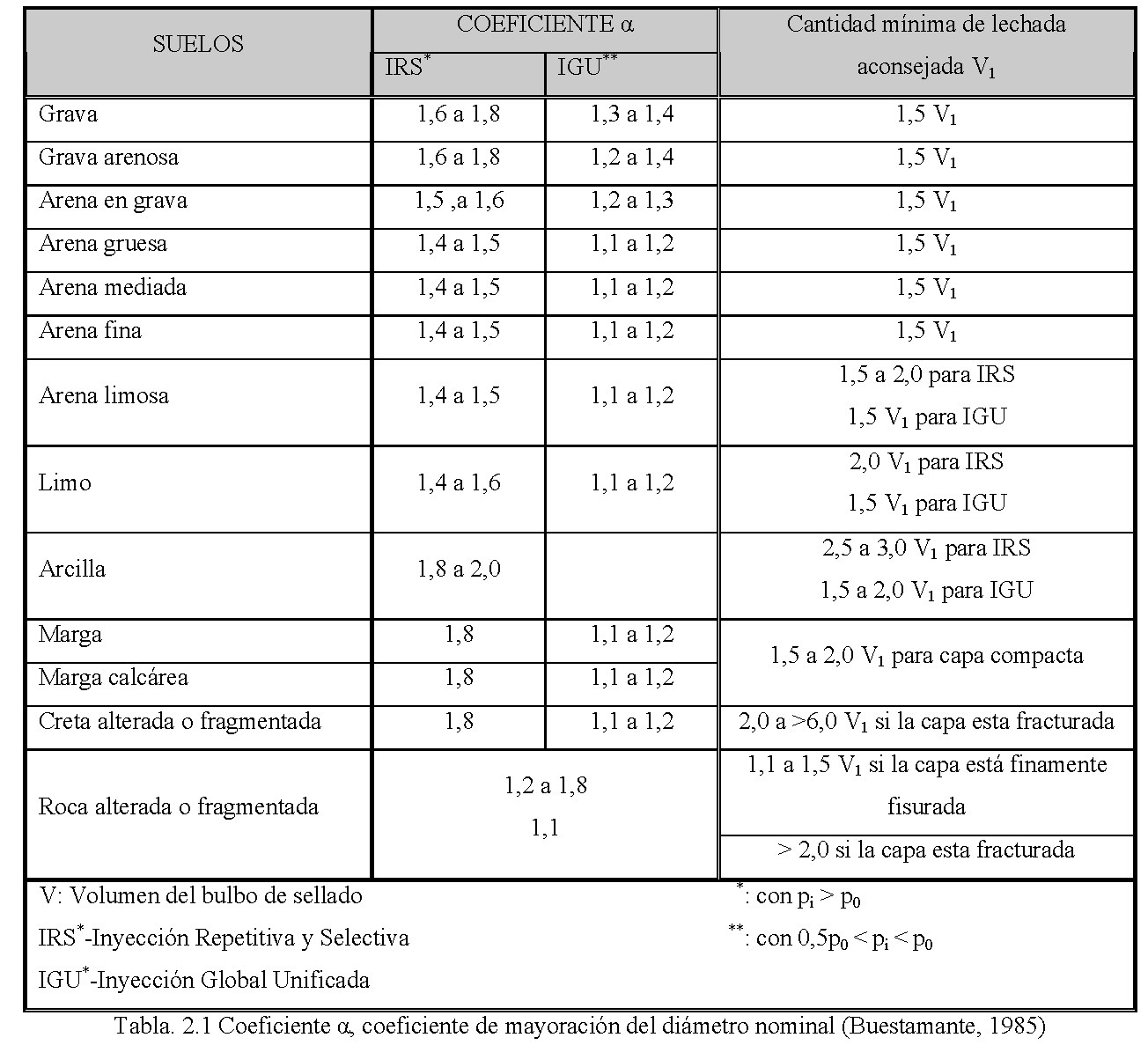
Como se puede ver el tipo de inyección también influye en el valor a considerar.
El segundo de los trabajos presentados por el Belgian Building Research Institute que resume más de 30 ensayos in-situ realizados. Los valores son similares a los de Bustamante.
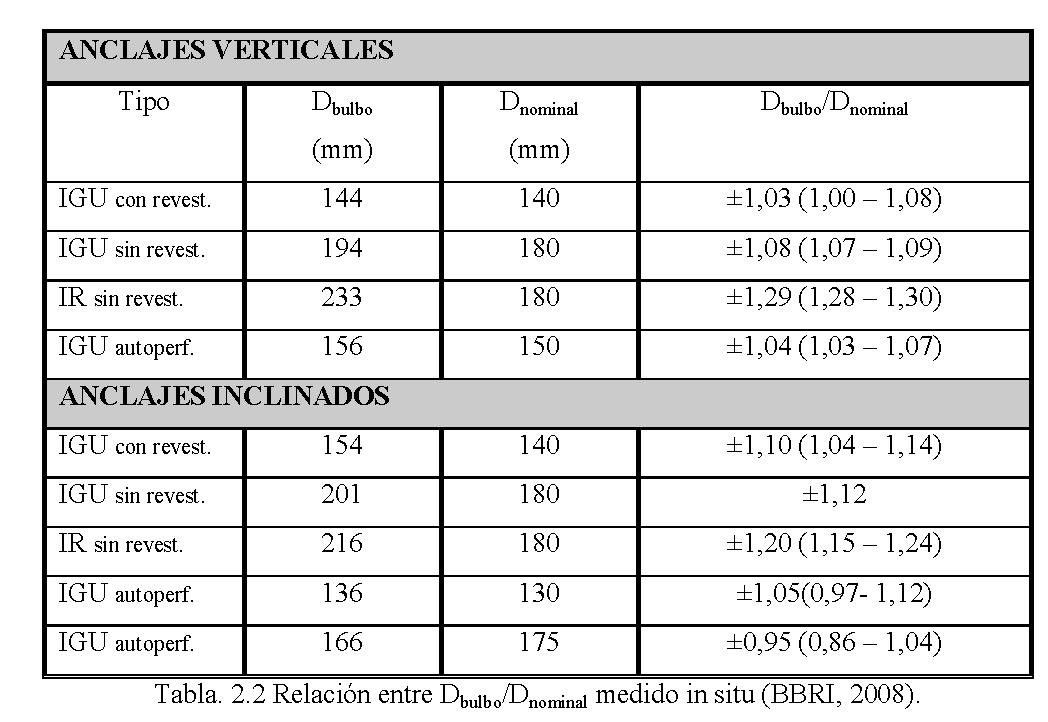
Medidas correctoras de deslizamientos de taludes
No e sencillo establecer unas actuaciones correctoras estándar para la inestabilidad de los talunes. Para cada caso se deben estudiar las medidas de acuerdo con los problemas concretos de cada caso, en función de sus características específicas.
Pero en esta entrada se quiere indicar un posible “catálogo” de posibles actuaciones que se para mejora de la estabilidad de taludes de desmonte. La única utilidad es que cuando estudiemos un desmonte las tengamos todas presentes.
- Movimientos de tierras: retaluzado con una pendiente más suave.
- Mejora de las condiciones de drenaje:
- Drenaje superficial: revestimiento de cunetas de coronación y pie de desmonte, impermeabilización de bermas, bajantes revestidas, etc.
- Drenaje profundo: fundamentalmente, drenes californianos.
- Refuerzo con gunitado/hormigón y bulones/anclajes
- Protección superficial con gunitado.
- Gunitado de zonas discontinuas, con refuerzo de bulones.
- Refuerzo con bulones exclusivamente (sin gunitado).
- Gunitado de grandes superficies (incluso de taludes completos) con bulonado.
- Muros de hormigón armado, anclados.

- Escolleras
- Chapado de protección en el pie de los taludes.
- Rellenos de escollera en el talud para corrección de inestabilidades o saneo de zonas con surgencia de agua.
- Repié o muro, para añadir peso en la parte baja del talud.
- Mallas
- De guiado de caída de piedras.
- De refuerzo (ancladas mediante bulones).
- Actuaciones singulares
- Pozos verticales.
- Pantalla de pilotes
Erosión en taludes
La erosión se puede definir como el proceso de desprendimiento y arrastre acelerado de partículas de suelo causado por el agua y el viento. Si se supera la resistencia al corte del suelo y las partículas se desprenden.
En la erosión hídrica el agua arranca y transporta partículas de suelo. Dependiendo de la importancia del fenómeno se producen regueros, cárcavas, inestabilidades. Es decir, en ocasiones los fenómenos se estabilizan. En otras ocasiones puede producir la rotura progresiva del talud. Influye la intensidad, duración y frecuencia de la lluvia. Se produce, evidentemente, en climas lluviosos. Es especialmente importante si son lluvias torrenciales, tormentas. También del tipo de suelo, la resistencia al corte del mismo.
En la erosión eólica el viento disgrega, altera y transporta partículas. Estas propias partículas arrastradas por el viento incrementan el proceso erosivo. Se suele producir en suelos sueltos y textura fina, lluvias escasas, temperaturas altas, vientos fuertes. Y en materiales que se alteran a la intemperie. Por ejemplo, en climas desérticos.

Bajante en una zona de humedad del talud que evita la erosión
Las medidas correctoras que pueden evitar/minimizar los efectos de la erosión interna pueden ser:
- Conducir el agua adecuadamente para evitar que pueda circular por la propia superficie del talud.
- Modificación de la topografía. Los taludes más tendidos reducen la velocidad del agua por el talud y, por tanto, reducen su efecto erosivo.
- Implantación de vegetación. En ocasiones hay que aportar tierra vegetal para que la vegetación pueda crecer.
- Implantación arbórea o arbustiva.
- Realización de hidrosiembra (proyección de una dispersión de celulosa, abonos y mezcla de semillas). Hay que poner especies de la zona para que puedan crecer.
- Colocación de láminas o elementos artificiales de protección. Así se evita que agua circule directamente sobre el talud.
- Implantación de medidas químicas (estabilizadores, asfalto, protectores químicos, sellantes)
- Gunitado (hormigón proyectado)
- Revestimiento con piedras o bloques de hormigón. Además de evitar la erosión, actúan como filtro que impide la pérdida de partículas.
- Colocación de fajinas (clavado de hierros o estacas de madera a las que se fijan redes de materiales plásticos, ramas..)
- Implantación de medidas mecánicas (elementos de drenaje, muros, refuerzos…)
- En la erosión eólica se pueden colocar obstáculos que corten el viento (pantallas, paneles)
- En taludes en arcillas la erosión en el pie por circulación de agua puede producir al ruina del talud. Se produce una rotura remontante. Para evitarla se suele colocar una escollera en el pie que sirva de elemento de contención en el pie y evite los arrastres.



