Cálculos con programas de equilibrio límite
En esta entrada quiero compartir algunas ideas que debemos conocer cuando empleemos un programa de equilibrio límite para estudiar la estabilidad de una excavación, la seguridad de una presa o de un terraplén…
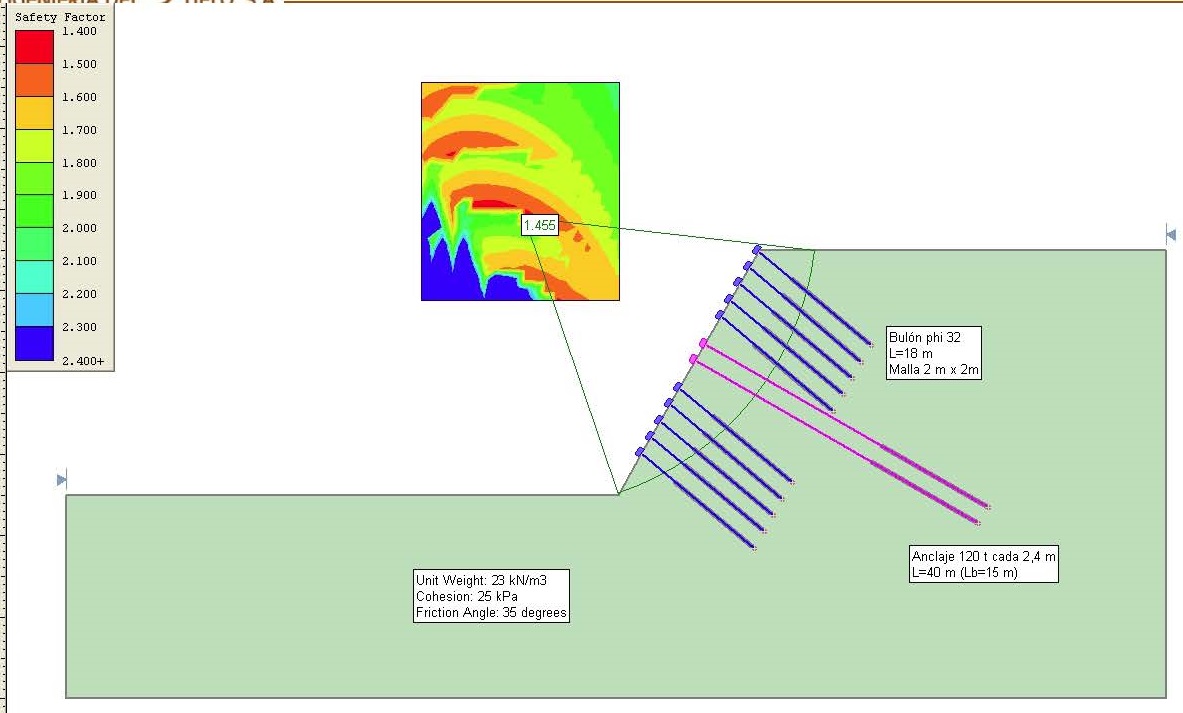
Una de las limitaciones de este tipo de cálculo es que sólo es posible llevar a cabo cálculos bidimensionales (en deformación plana). En muchos cálculos esto no será un inconveniente.
En el caso del método del equilibrio límite, una vez definidos los datos se han de introducir posibles superficies de deslizamiento, que pueden ser círculos, tramos rectilíneos unidos o combinación de ambos. El programa calcula el coeficiente de seguridad para cada una de las superficies introducidas, suponiendo que el coeficiente de seguridad es constante a lo largo de la misma. Suele ser habitual tantear superficies circulares.
Para calcular el coeficiente de seguridad, los programas basados en el equilibrio límite divide en rebanadas, mediante líneas verticales, el área comprendida entre la superficie de deslizamiento introducida y la superficie del terreno. Para cada rebanada calcula el diagrama de fuerzas actuantes y plantea un sistema de ecuaciones a resolver.
Con los datos introducidos (cohesión, fricción, densidad, geometría), no se puede resolver el sistema de ecuaciones planteado, siendo necesario conocer más datos o realizar hipótesis, concretamente la dirección, magnitud y/o punto de aplicación de algunas fuerzas.
Existen varios procedimientos para resolver el sistema de ecuaciones planteado (Morgenstern-Price, Spencer, …). A modo de resumen, en la Tabla I se presenta un breve resumen de los métodos de cálculos realizado por Frediund en 1984.
Tabla I.- Métodos de cálculo
| Método | Equilibrio de fuerzas | Equilibrio momentos | Hipótesis | |
| Dirección 1 | Dirección 2 | |||
| Fellenius | Sí | No | Sí | Sólo equilibrio según la dirección perpendicular. Se desprecian las fuerzas entre rebanadas |
| Bishop simplificado | Sí | No | Sí | Sólo equilibrio según la dirección vertical. Las fuerzas entre rebanadas son horizontales |
| Janbu simplificado | Sí | Sí | No | Sólo equilibrio según la dirección vertical. Las fuerzas entre rebanadas son horizontales. Se añade un factor corrector |
| Spencer | Sí | Sí | Sí | Inclinación constante entre las fuerzas entre rebanadas |
| Morgenstern-Price | Sí | Sí | Sí | La dirección de las fuerzas entre
rebanadas se define de una manera arbitraria. |
La fuerza normal N puede alcanzar valores no razonables debido a que el denominador sea próximo a cero o negativo (se puede producir cuando la salida de la línea de rotura se encuentra en contrapendiente). Cuando el denominador se aproxima a cero la fuerza normal que resulta llega a ser desproporcionada. Como resultado, la resistencia al corte movilizado es muy grande lo que conduce a coeficientes de seguridad muy elevados. Si el denominador es negativo la fuerza normal en la base de la rebanada se convierte en negativa lo que produce que el coeficiente de seguridad disminuya hasta valores próximos a cero que no tienen un significado real.
Como se acaba de ver los problemas de convergencia son debidos, principalmente, a una geometría de la superficie de rotura inapropiada. Para evitar esta cuestión se puede aplicar la teoría clásica de empujes de tierra para determinar la forma de la superficie de rotura. De acuerdo con esta teoría el terreno es dividido en dos zonas: activa y pasiva. La inclinación de la superficie en la zona pasiva debe ser limitada a 45 – Ø/2 y en el otro extremo de la línea de rotura (zona activa) la inclinación no debe superar el siguiente límite 45 + Ø/2
Si se aplican estas limitaciones a la geometría de la superficie de rotura no suelen aparecer problemas de convergencia en el cálculo.
Además de las superficies de rotura circulares se deben tantear superficies poligonales. Este tipo de líneas pueden ser las más desfavorables si existe algún estrato débil en el cimiento, la existencia de un tapiz bajo el espaldón de una presa… Pero ojo que las superficies poligonales pueden conducir a resultados engañosos si no aseguramos que sean superficies cinemáticamente posibles.
Existen otras variables de cálculo que también deben ser analizadas para comprobar su influencia en el cálculo. Entre otras, serían las siguientes; relación entre la fuerza normal y tangencial de la rebanada, considerar como rígida o flexible la cimentación, el método de cálculo (Bishop, Morgenstern-Price, Spencer…). Se ha comprobado que la influencia de estas variables es pequeña en el resultado de la carga de hundimiento de una cimentación superficial.
Por último, se ha comprobado, que si la discretización es poco detallada (número de rebanadas pequeña) los resultados quedarían del lado de la seguridad.
Permeabilidad en calicatas: ensayo Haefeli
En ocasiones puede resultar interesante la obtención de la permeabilidad de un suelo mediante ensayos de permeabilidad en calicatas. El ensayo más realizado es el propuesto por Haefeli o método de la artesa. En dicho ensayo la calicata se excava según un tronco de pirámide cuadrada, cuya cara inferior tiene 0,5 m de lado y la superior 1,5 m. La altura de la pirámide (de la calicata es 0,5 m).

En el ensayo se aporta un cierto caudal a la calicata hasta que el nivel se mantiene constante con el tiempo, es decir, alcanzando un régimen permanente. Si se denomina b al ancho inferior de la calicata (0,5 m) y h a la altura de la lámina de agua respecto a la base de la calicata, se estima el coeficiente de permeabilidad mediante la siguiente expresión:
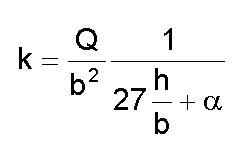
Siendo α el coeficiente de capilaridad que es del orden de 3.
Como se puede observar para la realización de este ensayo se debe colocar una escala vertical en el fondo de la excavación para poder establecer la altura del agua en la calicata.
Si no se pudiera alcanzar un régimen permanente, se puede estimar el coeficiente de permeabilidad para una situación transitoria entre con la siguiente expresión:
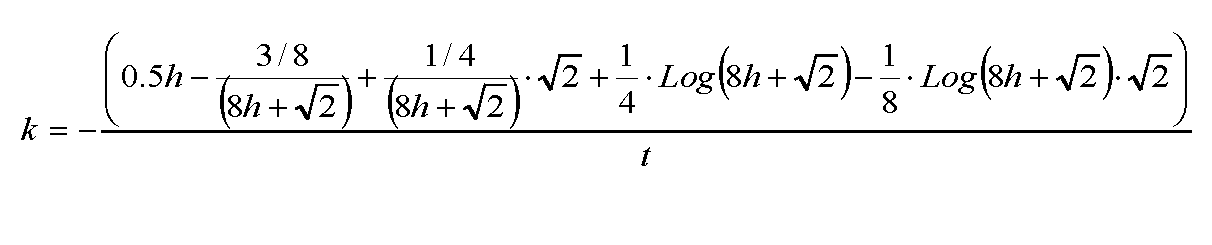
En esta expresión h sería la diferencia entre la altura del agua en el tiempo t1 y en t2. Y la variable t es igual a la diferencia t1-t2.