COEFICIENTE DE BALASTO EN PASOS INFERIORES
Las cargas o tensiones medias transmitidas bajo estos pasos inferiores que corresponden a un marco cerrado son menores que las del terraplén en el que quedan integradas.
Para el cálculo de estas estructuras el único parámetro relevante, a los efectos de realizar el cálculo de la estructura, es el coeficiente de balasto vertical. Realmente este coeficiente, que corresponde a la relación entre la presión y el asiento.
El módulo de balasto, por tanto, no constituye una propiedad geotécnica del terreno, sino que es un artificio de cálculo (que facilita el empleo de los programas de cálculo de estructuras). Por ello, su utilización y los valores asignados al mismo deben tener en cuenta diversos aspectos adicionales (dimensiones del área cargada, estratigrafía del terreno, etc..).
Por otro lado, cuando se estiman los asientos bajo la estructura, no se consideran los inducidos por el incremento de tensiones producido por las tierras adosadas. También hay que tener en cuenta que una parte de los asientos se debe al acortamiento producido en niveles profundos que no producirán asientos diferenciales al nivel de apoyo de la estructura y, por tanto, no inducirán esfuerzos en la losa.
En cualquier caso, este modo de estimar los esfuerzos en la losa inferior está ampliamente difundido en el cálculo de este tipo de estructuras.
El procedimiento empleado para obtener el módulo de balasto se basa en caracterizar los niveles de apoyo suponiendo un modelo elástico lineal (E, módulo de elasticidad y coeficiente de Poisson, ν) y estimar los asientos. Existen diversas fórmulas analíticas para estimar el valor del asiento. Ente otras, la siguiente:
Kv = p/s = (E·b) / [(1-ν2)·(B·L)0,5 ]
donde:
p = presión aplicada
s = asiento de la cimentación
B = ancho de la losa
L = longitud de la losa
b = 1,07 coeficiente de forma para L=B, Davis&Poulos (1973)
E = módulo de elasticidad del terreno
ν = coeficiente de Poisson
Los niveles superficiales del terreno tendrán un módulo relativamente bajo. No obstante, en general, la profundidad de apoyo de la losa es del orden de 1.0-1.5 m, si bien esta profundidad varía en cada caso particular.
Para tener un cierto orden de magnitud del valor del módulo de balasto se supondrá un módulo de deformación de unos 500 kp/cm2. El valor del módulo de Poisson que se considera es de 0.3, el ancho de la losa de 10 m y el espaciamiento entre juntas también de 10 m. Con estos valores resulta el siguiente módulo de balasto:
Kv = p/s = (E·b) / [(1-ν2)·(B·L)0,5 ]= 600 t/m3
El valor de referencia que se supondrá como módulo de balasto para la comprobación de las losas de apoyo de los marcos será de 500 t/m3. Valores de módulos de balasto inferiores al indicado no conllevan un incremento de esfuerzos significativos.
En cada marco se analizaran las condiciones específicas de apoyo y se recomendarán las medidas necesarias para garantizar un apoyo homogéneo sobre un nivel de compacidad media. Para lo cual se propondrán, cuando se considere necesario, sustituciones, recolocaciones, etc. De este modo, se evitan reacciones puntuales y se mejoran las condiciones de apoyo en las zonas donde los niveles superficiales resulten de compacidad baja.
Asiento de consolidación
En esta breve entrada se puede comprobar que el asiento por consolidación para un incremento de tensión no depende del espesor de la capa si el grado de consolidación es menor que el 60%. Jesús, ¿seguro que es verdad? No parece intuitivo.
Vamos a verlo a continuación.
Para un tiempo t desde la aplicación de la carga el asiento se podría calcular con la siguiente expresión:
st = s∞ · u (%)
Como el valor a tiempo se puede poner en función de la tensión, del módulo edométrico y del espesor de la capa, la expresión anterior se puede expresar como sigue:
st = Δσ/Em· H u (t)
Si el grado de consolidación es inferior al 60% el grado de consolidación de puede expresar de la siguiente forma si la distancia de drenaje fuera igual a H (drenaje sólo por una cara del estrato):
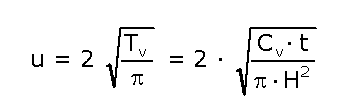
Y, por tanto, el asiento en un tiempo t resultaría:
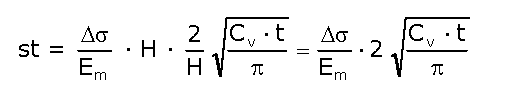
Como se puede comprobar el asiento en el tiempo t no depende del espesor del estrato. Si el espesor es mayor el grado de consolidación será más pequeño, pero el asiento el mismo.
Hundimiento de una placa de carga
La placa de carga es un ensayo que nos permite comprobar el grado de compactación del material. En ocasiones, se han realizado placas de carga en una zona inundada con agua para estudiar el posible colapso del material.
A continuación comparto un caso real que nos va a confirmar cómo las presiones intersticiales producen una disminución de la resistencia.
Durante la carga inicial de un ensayo de placa de carga se evidenciaron síntomas de rotura del terreno: aparecieron grietas cuando se cargó la placa a unas 24 t/m2 y se registró un elevado asiento cuando se alcanzó una carga de unas 35 t/m2. Este ensayo se había realizado con material colocado del lado húmedo.
Sin embargo, anteriormente se había realizado la placa de carga del lado seco sobre el mismo terreno y éste no había colapsado para esas cargas. De hecho, se consiguió cargar la placa hasta 50 t/m2. Esto significaría que la carga de hundimiento debería ser superior a 50 t/m2. De hecho el cálculo teórico mediante la expresión de Brinch Hansen conduciría a un valor de la carga de hundimiento de 120 t/m2.
Ante esta situación cabe preguntarse: ¿por qué se produjo el inicio de la rotura para cargas del orden de 25-35 t/m2 en el ensayo que se hizo del lado húmedo y no ocurrió esto en el ensayo que se hizo seco?
La respuesta a esta pregunta hay que buscarla precisamente en las condiciones de humedad del terraplén. Las determinaciones de humedad que se realizaron in situ antes de la ejecución de la placa de carga mostraron una humedad media del material del orden del 15%. Esto significa que, asumiendo un peso específico del material de 2 t/m3, un volumen de 1m3 de material contiene 2000 kg de terreno y 0.15 · 2000 = 300 litros de agua.
Se trata de un volumen de agua importante. De hecho, para un peso específico de las partículas de valor G = 2.72 t/m3, y para un valor de la densidad seca de γd = 1.85 t/m3, una humedad de valor W = 15% implica un grado de saturación próximo al 90%.
Para humedades de saturación de este orden, lo que ocurre es que al cargar un terreno, el agua que existe en él también se comprime junto con el propio material del terreno, es decir, que se generan presiones intersticiales. Estas presiones intersticiales originan una reducción en la cohesión del terreno, del tal forma que la cohesión de cálculo con la que habría que entrar en la fórmula de Brinch Hansen para considerar la generación de presiones intersticiales sería:
c cálculo =c terreno – u tan Φ
siendo u la presión intersticial que se genera durante el proceso de carga y Φ el ángulo de rozamiento interno del material.
De esta forma, con que se generasen presiones intersticiales de valor medio u = 1.5 t/m2 (situación bastante probable), la cohesión quedaría reducida aproximadamente a la mitad (se pasaría de c = 2t/m2 a c = 1t/m2). Esto explicaría por qué para una carga aplicada de valor inferior a la carga de hundimiento comienzan a aparecer grietas en el terreno y deformaciones elevadas.
Con este caso real sencillo he querido reflejar una vez más la importancia de las presiones intersticiales en el comportamiento del terreno.



