Inicio » Artículos publicados por daniel.duque@upm.es (Página 2)
Archivo del Autor: daniel.duque@upm.es
Puesto para investigador Ramón y Cajal
Se ofrece un puesto de investigador dentro del la convocatoria del Programa Ramón y Cajal.
El investigador se integraría dentro del grupo de investigación CEHINAV.
Los interesados se pueden poner en contacto con
daniel [punto] duque [arroba] upm [punto] es
Las líneas son las siguientes:
- Experiencia con el software de CFD OpenFOAM, de código abierto
- HPC para uso en Mecánica, Mecánica de Fluidos, Biomécanica, Estructuras, etc.
- Desarrollo de métodos CFD sin malla ("meshless")
- Análisis de métodos numéricos
- Aplicación de métodos de dinámica de fluidos computacional (CFD) a la hidrodinámica de buques
- Análisis y optimización de formas de buques mediante estudios numéricos o experimentales
- Estudios numéricos o experimentales de la hidrodinámica en artefactos y plataformas marinas
- Investigación computacional o experimental del fenómeno de movimiento de fluidos confinados ("sloshing")
Más información sobre el programa en la página de la UPM dedicada al mismo.
Análisis de estabilidad de von Neumann
Este método es muy conocido para analizar los parámetros en una discretización que garantizan la estabilidad del método numérico. Ver, por ejemplo, el análisis de la ecuación de difusión en wikipedia (que yo, ejem, acabo de modificar). Pero, en mi opinión, la discusión se mete en funciones trigonométricas que despistan bastante. Sobre todo, porque acaban evaluadas en "la peor situación", que se ve venir de antemano. Aquí propongo anticipar esa situación desde el principio.
Por cierto: es "fon no i man"
Presentaciones rápidas y fáciles con reveal.js
A menudo es necesario generar una presentación para un congreso o curso en poco tiempo, pero que cumpla estas características
- Que sea visualmente atractiva
- Que incluya matemáticas facilmente (en LaTeX, a ser posible)
- Que esté "en la nube"
- Que pueda incluir películas
Aquí cuento una opción muy sencilla, que utiliza:
- El entorno reveal.js
- El lenguaje markdown
- El servicio github para subir cosas a un host fácil y rápidamente
El resultado puede verse en las transparencias para el curso Métodos Numéricos en Mecánica de fluidos o la presentación sobre el artículo … phase separation kinetics for … two-dimensional membranes.
reveal.js
Este entorno fue creado por el sueco Hakim El Hattab para generar presentaciones que pueden verse con un navegador. Se puede usar de forma local, abriendo las páginas, que están en nuestro ordenador, con un navegador, o subir las páginas a algún host (como explico más abajo).
Lo más sencillo es "clonar" reveal.js a nuestro disco local y modificar los ficheros index.html o demo.html que vienen con la distribución
markdown
Cuando editamos estos ficheros nos encontramos con html bastante fácil de entender:
<section>
<h2>Touch Optimized</h2>
<p>
Presentations look great on touch devices, like mobile phones and tablets. Simply swipe through your slides.
</p>
</section>
Por ejemplo, cada transparencia está delimitada por "<section>". Podemos entonces introducir texto html directamente, pero para los impacientes como yo es muy interesante usar markdown:
<section data-markdown>
## Markdown supportWrite content using inline or external Markdown.
Instructions and more info available in the [readme](https://github.com/hakimel/reveal.js#markdown).
</section>
La transparencia empieza con "<section data-markdown> <script type="text/template"> " , y lo que contiene es texto en formato markdown. Sin entrar en detalles, es una manera facilísima de maquetar texto para las tareas habituales (listas, encabecamientos, enlaces url, LaTeX). Por ejemplo:
<section data-markdown>
<script type="text/template">
#### Discretization : steady 1D diffusion
To illustrate how the conservation equations used in CFD can be discretized, we will look the diffusion of a chemical species
(constant density, incompressible flow), given by:$$
\frac{d}{{dx}}\left( {D\frac{{dc}}{{dx}}} \right) + S = 0
$$
Here $c$ is the concentration of the chemical species, $D$ is the diffusion coefficient, and $S$ is a source term
</script>
</section>
Markdown es tambiénmuy conocido porque se usa para generar los ficheros de ayuda README.md en github y otros sitios. En todo caso, mucho más fácil que html. El único pero es que algunas ecuaciones LaTeX no se compilan bien; para ello hay que escribir “ antes de la ecuación. Por ejemplo:
<section data-markdown>
<script type="text/template">
#### Discretization : steady 1D diffusion
<img src="FVM_1D_cells.png" style="background:white" width="40%">
“$$
\left( DA\frac{dc}{dx} \right)_e \doteq D_e A_e \frac{c_E – c_P }{\delta x_{PE}}
$$“
$
D_e \doteq \frac{{D_E + D_P }}{2}
$
$
\overline S \Delta V: = S_u + S_P c_P
$
</script>
</section>
(también se incluye una imagen, mediante html)
github
Ojo: Este proceso es para un sistema linux y con un github ya configurado para subidas y bajadas automáticas (por ssh). Eso es otra historia, pero no es difícil y está bien explicado en muchos sitios, p.e. en la página oficial (en inglés, eso sí).
Ya hemos mencionado el servicio github porque reveal.js está albergado en él. Se trata de un servicio extremadamente interesante para proyectos colaborativos. Es muy conocido para programación, pero se puede usar perfectamente para transparencias, documentos, etc. Además no es necesario que los proyectos sean colaborativos, incluso para un solo usuario es interesante al ser un servicio de nube gratuito y muy optimizado. Eso sí, sólo para proyectos abiertos, si no hay que pagar, o se puede usar otro servicio, como bitbucket.
Lo interesante es que github ofrece un servicio web hosting gratuito y muy sencillo. Si nuestro usuario se llama ddcampayo, e inicia un repositorio llamado ddcampayo.github.io, el dominio https://ddcampayo.github.io/ automáticamente muestra los contenidos del repositorio. Esto es enormemente cómodo. El proceso típico sería así:
- En nuestro ordenador tenemos un directorio llamado igual que el proyecto, p.e. ddcampayo.github.io. En él editamos los ficheros que queramos (ficheros html para reveal.js, por ejemplo) y colocamos gráficos, gifs animados, películas, pdfs…
- Vamos visualizando los cambios con un navegador que abre los ficheros locales ("file://" en el campo url, en vez de "http://")
- Cuando nos guste, subimos los cambios con git commit -m 'descripcion de mis cambios' seguido de git push
- Ya está, al cabo de unos segundos los archivos aparecen en la página web, por ejemplo, https://ddcampayo.github.io, y todo el mundo puede verlos
También podemos usar otro ordenador para hacer cambios, o la interfaz web de github, pero hay que acordarse de hacer "git pull" en los ordenadores que no están actualizados a la última versión.
OpenFOAM en Virtualbox
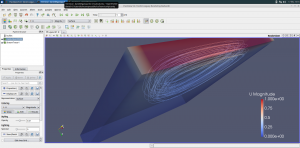 Aquí explico cómo correr una máquina virtual linux ("huesped") en un entorno ("anfitrión") windows para tener OpenFOAM.
Aquí explico cómo correr una máquina virtual linux ("huesped") en un entorno ("anfitrión") windows para tener OpenFOAM.
Primero, instalamos virtualbox. Lo abrimos, damos a "nueva", "modo guiado" (el experto tampoco es mucho más difícil), Luego, escogemos un sistema linux, ubuntu 64 bits (salvo que nuestro PC sea de 32, claro). Puede que no aparezca la opción de 64 bits la primera vez que corremos virtualbox. Si lo cerramos y abrimos de nuevo, ahí estará (???). Asignamos una buena cantidad de memoria a la máquina virtual, 4Gb mínimo. En realidad, lo normal es ver cuánta memoria se usa en el entorno anfitrión haciendo lo habitual (al menos, estará windows y seguramente un navegador con algunas pestañas abiertas).
Luego, hay que crear un disco duro virtual. Usar VDI, la opción sugerida. El disco duro es mejor que sea "dinámico"; el anfitrión lo ve como un fichero que va creciendo o menguando según haga falta. Luego, el tamaño, lo mínimo en nuestro caso sería 8Gb (¡el sistema y OpenFOAM se "expanden" hasta los 5Gb al instalarse!), pero entonces NO hay que crear partición de swap en linux (ver más abajo). Si no, lo mínimo son 8+(tamaño de RAM). En realidad, como el disco es dinámico se puede escoger un tamaño muy grande (p.e. 128Gb) y tener cuidado con no llenarlo (las simulaciones, de hecho, pueden llenar un disco duro en minutos).
Una vez configurado el disco duro, hay que configurar el sistema (todas estas opciones se pueden cambiar después, pero es buena idea dejarlas listas ahora). Pulsar en "configurar".
En "General", "avanzado", es útil "compartir portapapeles". Yo lo pongo en "bidireccional", para cortar y pegar texto entre el sistema anfitrión y el virtual (no he probado nunca a cortar y pegar ficheros y cosas así…). En "sistema" se puede cambiar la memoria base, y asignar más procesadores de los que tengamos a la máquina virtual (pestaña "procesador").
En "Pantalla", subir los ridículos 16Mb asignados a la tarjeta de vídeo al máximo (128Mb, que tampoco es tanto). Asegurarse de que NO está seleccionada la aceleración 3D, de momento paraview no funciona con esta opción (es decir, ni a mí ni a muchos nos funciona, pero se puede probar a ver).
En "Almacenamiento", añadir un CD IDE (icono de CD con un signo "+"), "Seleccionar disco", y navegar hasta la imagen ISO. Virtualbox montará esta imagen como un disco virtual adicional desde el cual podemos arrancar el sistema. Se puede usar la imagen ISO que yo he creado, que ya tiene OpenFOAM instalado. Pero la máquina virtual accede a internet a través del anfitrión, así que se puede también usar una imagen cualquiera de cualquier variante de ubuntu y luego instalar OpenFOAM como se explica en la documentación oficial.
También es muy interesante "Carpetas compartidas". Seleccionamos "+", una carpeta a la que tengamos acceso (puede ser nuestra carpeta raíz, pero quizá sea un poco arriesgado, mejor crear un directorio de intercambio ad hoc; otra opción tentadora es compartir la carpeta de dropbox o owncloud). Quitar "solo lectura" y poner "automontar". Poner un nombre sencillo, p.e. "share". Más adelante, desde ubuntu, hay que correr lo siguiente:
sudo mount -t vboxsf -o uid=$UID,gid=$(id -g) share ~/host
Donde "share" es el nombre de la carpeta compartida y ~/host es el directorio donde queremos que aparezca ("~" significa "directorio raíz de usuario"). Es un comando un poco feo, así que se puede usar un alias
Por fin, encendemos la máquina virtual ("Iniciar"). Debería arrancar directamente del iso. Se trata de una instalación ubuntu estándar, muy rápida y sencilla. Lo único, cuando llegue el momento de particionar el disco duro, debemos seleccionar la opción manual si no queremos swap. Luego, crear una sola partición con el tamaño máximo (creo que no hace falta en estos casos meterse con particiones de sistema y usuario, etc), y aceptar el mensaje relativo a no crear swap. Por lo que he leído, últimamente no es necesario gracias a la gran cantidad de RAM que tienen los equipos (al revés, paginar en disco tanta swap acaba ocupando una parte no despreciable del disco que quizá no se use nunca).
Cuando termine de instalarse el sistema, hay que reiniciar. Puede que la primera vez salga una pantalla horrorosa. No hay problema, con ctrl alt F1, ctrl alt F7 salimos a modo texto y volvemos a modo gráfico correctamente. Se supone que esto pasa sólo la primera vez, al menos si hacemos lo siguiente…
Que es instalar las "guest additions". Se trata de (otro) disco virtual tipo CD que contiene utilidades muy interesantes para Virtualbox. Como es habitual en ubuntu, aparecerá un icono con forma de CD en el escritorio. Podemos abrirlo con doble click, luego botón derecho sobre la zona blanca (no sobre un fichero o directorio), y correr
sudo ./VBoxLinuxAdditions.run
Este es un buen momento para usar [tab]: teclear “sudo ./” e ir probando qué pasa si vamos dando a [tab] una vez o dos …
Cuando se haya instalado, hay que reiniciar la máquina virtual.
Creo (no estoy seguro) que también conviene ir al menú del ratoncito (en xubuntu), arriba a la izquierda, y teclar "drivers" o "controladores". Seleccionar "controladores adicionales" y seleccionar el controlador gráfico VirtualBox (de Inno TeK GmbH).
El resto, como ya he explicado antes: ahora toca familiarizarse con el entorno. Si todo va bien, acaremos con un sistema capaz de correr OpenFOAM y de visualizar los resultados con paraview, como en la captura de pantalla que he puesto al principio.
Aunque la máquina es virtual, pulsando host + F pasamos a pantalla completa, y es habitual olvidarse de que el sistema es en realidad virtual. La tecla "host", por cierto, está asignada al ctrl derecho, aunque puede cambiarse. Para volver al modo de ventana, puede pulsarse host + F de nuevo, o ir con el ratón abajo y al centro, con lo que aparece un menú oculto de Virtualbox.
Primera sesión con linux y openfoam
Este tutorial supone que tenemos una distrubución xubuntu 16.04LTS con OpenFOAM4.1 instalado (en realidad, vale para cualquier variante de ubuntu y cualquier versión de OpenFOAM que no sean muy antiguos).
Se puede obtener una imagen iso que yo he creado en este enlace. En una entrada anterior he descrito cómo crear la imagen y cómo "quemarla" en un USB, de modo que podamos hacer todo esto sin necesidad de instalar linux permanentemente en un ordenador.
Lo primero, abrimos "File manager" del menú xubuntu (ratoncito azul arriba a la izquierda). Y luego, "Terminal emulator". En el segundo,
ls
Vemos que nos da una lista de directorios que coincide con File manager. Probar también
ls -l
ls -a
ls -al
El directorio que contiene OpenFOAM es /opt :
ls /opt/
"/" significa "raíz del disco. Probar "ls /".
OpenFOAM no está "instalado" de serie, para acceder a todo hay que correr un fichero cada vez que se entra en linux:
. /opt/openfoam4/etc/bashrc
Más adelante veremos que esto puede automatizarse con un fichero de arranque. ". " significa "ejecutar, correr". ¡Ojo al espacio! También puede correrse "source /opt/openfoam4/etc/bashrc", es lo mismo.
Ah, es hora de practicar la autocompleción con el tabulador. Es mejor teclear ". /o", dar al tabulador y se completa como ". /opt/", ya que es la única opción. En cambio, ", /" no completa nada cuando se pulsa tabulador una sola vez. Una segunda vez nos muestra las opciones posibles. Muy muy útil.
Ahora aparen comandos que antes no teníamos. Por ejemplo "block" + [tab] dos veces nos da "blockdev blockMesh". El primer comando ya estaba antes, pero el segundo es una utilidad de OpenFOAM. Si preguntamos dónde está
which blockMesh
queda claro:
/opt/openfoam4/platforms/linux64GccDPInt32Opt/bin/blockMesh
echo $FOAM_RUN
mkdir -p $FOAM_RUN/
cd $FOAM_RUN/
ls
cd
cd –
ls
pwd
cd ..
ls
cp -r $FOAM_TUTORIALS/ .
cd tutorials/incompressible/icoFoam/cavity/cavity
ls
blockMesh
paraFoam
icoFoam
Time = 0.055
Courant Number mean: 0.21382 max: 0.847682
smoothSolver: Solving for Ux, Initial residual = 0.0023784, Final residual = 6.13546e-06, No Iterations 11
smoothSolver: Solving for Uy, Initial residual = 0.00526521, Final residual = 7.98841e-06, No Iterations 12
DICPCG: Solving for p, Initial residual = 0.00564918, Final residual = 0.000273181, No Iterations 8
time step continuity errors : sum local = 2.32443e-06, global = 1.00259e-19, cumulative = -1.05705e-18
DICPCG: Solving for p, Initial residual = 0.00433468, Final residual = 9.31993e-07, No Iterations 27
time step continuity errors : sum local = 7.64137e-09, global = -6.73325e-19, cumulative = -1.73037e-18
ExecutionTime = 0.03 s ClockTime = 0 s
icoFoam > log &
Nuevo artículo, fecha: San Isidro 2017
Nuevo artículo aceptado: Extending linear finite elements to quadratic precision on arbitrary meshes, Daniel Duque, Pep Español, Jaime Arturo de la Torre (UNED, los dos últimos). Descargable gratuitamente hasta fin de febrero.
Fecha de "publicación" (en papel, supongo): 15 de mayo de 2017. ¡San Isidro!
Crear distribución ubuntu a medida
Para impacientes: en este enlace he puesto la image iso de la distribución, lista para descargar y "quemar" en un USB (ver más abajo sobre el quemado).
De momento, el ubuntu customization kit sigue siendo la manera más rápida y fácil de crear una distribución ubuntu a medida. En el artículo Cómo crear una distribución ubuntu a medida con uck está todo muy bien explicado.
Lo malo es que el proyecto está en estado de "discontinued" … además, no parece haber alternativa a día de hoy: alternativeto.net/software/uck/
Como era de esperar, por tanto, el proceso que se describe en el artículo anterior produce errores con distribuciones modernas.
Por suerte, en esta respuesta explican qué hacer:
- instalar el paquete gfxboot-theme-ubuntu
- instalar el paquete syslinux-utils si se quiere un ISO híbrido (la utilidad es "isohybrid")
- dejar en blanco las dos primeras preguntas sobre los lenguajes. En la tercera, es interesante escoger "es" para que funcione un teclado español
-
cambiar el fichero /usr/lib/uck/customization-profiles/localized_cd/customize_iso por lo que pego más abajo. Es buena idea, como de costumbre, hacer una copia de seguridad del fichero original:
sudo cp /usr/lib/uck/customization-profiles/localized_cd/customize_iso /usr/lib/uck/customization-profiles/localized_cd/customize_iso.backup
Grabación ("quemar")
El último paso es grabar el iso en un disco USB. Ellos recomiendan unetbootin tiene la opción "Space used to preserve files across reboots (Ubuntu only)". Como su nombre indica, crea un disco virtual con información que no se pierde entre distintas sesiones ("persistente"). También he probado mkusb, que parece muy completo y ofrece la opción de permanencia, además de la posibilidad de crear una partición de datos legible desde windows en el USB. También funciona el "startup disk creator", pero este no permite ya la opción que acabamos de comentar (antes, sí).
También puede grabarse desde windows, con utilidades como etcher, rufus o yumi. Por lo visto, ninguna de estas ofrece la opción de persistencia. La única que parece funcionar es lili usb. Para que ofrezca la opción de permanencia, hay que convencerle de que tenemos una distribución de tipo ubuntu; basta con cambiar el nombre al fichero iso para ello.
Por desgracia, he comprobado que un USB puede no funcionar en todos los ordenadores. De hecho, a veces funciona una primera vez, pero la segunda ya no, y además el USB se queda corrupto y no vuelve a funcionar más correctamente (se puede volver a utilizar, claro está, repitiendo con él el proceso).
El fichero corregido
#!/bin/bash
###################################################################################
# UCK – Ubuntu Customization Kit #
# Copyright (C) 2006-2010 UCK Team #
# #
# UCK is free software: you can redistribute it and/or modify #
# it under the terms of the GNU General Public License as published by #
# the Free Software Foundation, either version 3 of the License, or #
# (at your option) any later version. #
# #
# UCK is distributed in the hope that it will be useful, #
# but WITHOUT ANY WARRANTY; without even the implied warranty of #
# MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the #
# GNU General Public License for more details. #
# #
# You should have received a copy of the GNU General Public License #
# along with UCK. If not, see <http://www.gnu.org/licenses/>. #
#################################################################################### NAME:
# customize_iso — customize iso image outside of root FS
#
# SYNOPSIS:
# customize_iso [remaster_home] [customization_scripts_dir]
#
# DESCRIPTION:
# This procedure performs additional customization that needs to
# happen outside of the image of the root file system:
# – Configuration of the boot environment
# – isolinux configuration
# – gfxboot configuration (language/keyboard support!)
# – propagation of a new kernel/initrd
# – Simple bootmanager (directory "install" in image)
# – Configuration of additional resources outside the root FS
# – Add-Ons (like sample document/music/video files)
# – More Add-Ons (like OSS for Win / Mac)
#
# NOTES:
# Execution of the procedure may require Internet access to download
# the source of the latest version gfxboot-theme-ubuntu.
#
# If a local copy of gfxboot-theme-ubuntu is available in the remaster
# home, it will be used instead of a (possibly updated) download.SCRIPT_DIR=`dirname "$0"`
REMASTER_HOME=${1:-~/tmp}
SCRIPT_DIR=${2-$REMASTER_HOME/customization-scripts}
ISO_REMASTER_DIR="$REMASTER_HOME/remaster-iso"
REMASTER_DIR="$REMASTER_HOME/remaster-root"
BOOT_LANG=`cat "$SCRIPT_DIR/livecd_locale"`function failure()
{
echo "$@"
exit 1
}function get_latest_kernel()
{
set — $(ls "$REMASTER_DIR"/boot/vmlinuz* 2>/dev/null |
sed -e "s@$REMASTER_DIR/boot/@@" |
tr — '-.' '\t' |
sort –key=2 –key=3 –key=4 –key=5 –numeric-sort |
tail -n1 )
[ “$1” = “vmlinuz” ] && echo "$REMASTER_DIR/boot/$1-$2.$3.$4-$5-$6"
}# Create a temporary directory to assemble the gfxboot stuff in
BUILD_DIR=`mktemp -d`
if [ -d $REMASTER_HOME/gfxboot-theme-ubuntu ]
then
cp -r $REMASTER_HOME/gfxboot-theme-ubuntu "$BUILD_DIR" ||
failure "Cannot copy gfxboot-theme-ubuntu to $BUILD_DIR"
pushd "$BUILD_DIR" >/dev/null ||
failure "Cannot change directory to $BUILD_DIR"
else
pushd "$BUILD_DIR" >/dev/null ||
failure "Cannot change directory to $BUILD_DIR"
#—–HS (1)–>
#DISTRO_CODENAME=`cd "$ISO_REMASTER_DIR"/dists && find . -maxdepth 1 -type d | grep '/' | cut -d '/' -f2` ||
# failure "Unable to identify Ubuntu distro codename"
DISTRO_CODENAME="$(lsb_release -c|awk '{print $2}')"||
failure "Unable to identify Ubuntu distro codename"
#—–HS (1)–<
APT_SOURCES_TMP_DIR=`mktemp -d`
wget -c http://archive.ubuntu.com/ubuntu/ubuntu/ubuntu/dists/$DISTRO_CODENAME/main/source/Sources.gz -O "$APT_SOURCES_TMP_DIR"/Sources.gz
#—–HS (2)–>
#GFXBOOT_THEME_UBUNTU_SOURCE_PACKAGE=http://archive.ubuntu.com/ubuntu/ubuntu/ubuntu/pool/main/g/gfxboot-theme-ubuntu/$(zgrep gz "$APT_SOURCES_TMP_DIR"/Sources.gz | grep gfxboot-theme-ubuntu | sed -n 1p | awk '{ print $3 }')
GFXBOOT_THEME_UBUNTU_SOURCE_PACKAGE=http://archive.ubuntu.com/ubuntu/ubuntu/ubuntu/pool/main/g/gfxboot-theme-ubuntu/$(dpkg -l|grep gfxboot-theme-ubuntu|awk '{print $2"_"$3"_"$4".deb"}')
#—–HS (2)–<
wget $GFXBOOT_THEME_UBUNTU_SOURCE_PACKAGE ||
failure "Unable to download gfxboot-theme-ubuntu source package from $GFXBOOT_THEME_UBUNTU_SOURCE_PACKAGE"
#—–HS (3)–>
#tar xfz *.tar.gz ||
tar xfz *.tar.gz
dpkg -x *.deb . ||
failure "Unable to extract gfxboot-theme-ubuntu source package"
#—–HS (3)–<
fi# Build the gfx boot theme
#—–HS (4)–>
cd usr/share
#—–HS (4)–<
cd gfxboot-theme-ubuntu
cd po
ln -s pt.po pt_PT.po
cd ..
##if [ “$BOOT_LANG” = “pt_PT” ]; then
## make DEFAULT_LANG="pt" || failure "Failed to build gfxboot theme"
##else
make DEFAULT_LANG="$BOOT_LANG" || failure "Failed to build gfxboot theme"
##fi# Fix list of languages
pushd boot >/dev/null# Create regexp that matches all language packs on CD
langpack=""
for langpack in `cat "$SCRIPT_DIR/language_packs"`; do
if [ -z “$LANGPACKS” ]; then
LANGPACKS="$langpack"
else
LANGPACKS="$LANGPACKS|$langpack"
fi
done# Rewrite langlist
cat "$SCRIPT_DIR/livecd_locales" >langlist
popd >/dev/null# Copy to isolinux in image directory
cp -af boot/* "$ISO_REMASTER_DIR/isolinux/" ||
failure "Error while copying boot files to $ISO_REMASTER_DIR/isolinux"popd >/dev/null
# Cleanup
[ “$BUILD_DIR” != “/” ] && rm -rf "$BUILD_DIR"# Copy kernel and initrd, in case it was changed during installation
VMLINUZ=$(get_latest_kernel)
if [ “$VMLINUZ” != “” ]
then
INITRD="$REMASTER_DIR"/boot/initrd.img-$(echo `basename $VMLINUZ` | cut -d'-' -f 2-)
if [ -e “$VMLINUZ” -a -e “$INITRD” ]
then
echo "Updating kernel:"
echo " kernel=$VMLINUZ"
echo " initrd=$INITRD"
cp -f "$VMLINUZ" "$ISO_REMASTER_DIR/casper/vmlinuz"
cp -f "$INITRD" "$ISO_REMASTER_DIR/casper/initrd.gz"
else
echo "Not updating kernel as initrd not present"
fi
fi# Misc fixup for Karmic
pushd "$ISO_REMASTER_DIR"/isolinux >/dev/null# What used to be called "message" is now called "bootlogo"
if [ -f isolinux.cfg -a -n “`grep “gfxboot bootlogo” isolinux.cfg 2>/dev/null`” ]
then
if [ -f message ]
then
echo "Using bootlogo instead of message"
mv message bootlogo
fi
fi# What used to be a gzipped initrd now is a lzma compressed initrd
if [ -f text.cfg ] || [ -f txt.cfg ]
then
# At least one of the .cfg file will be missing. Drop error message.
lzused=`grep initrd.lz text.cfg txt.cfg 2>/dev/null`
lzmacmd=`which lzma`
if [ -n “$lzused” ]
then
if [ -n “$lzmacmd” ]
then
if [ -f ../casper/initrd.gz ]
then
pushd "$ISO_REMASTER_DIR"/casper >/dev/null
echo "Recompressing initrd from gzip to lzma"
rm -f initrd.lz
gunzip <initrd.gz | $lzmacmd >initrd.lz
rm -f initrd.gz
popd >/dev/null
fi
else
if [ -f ../casper/initrd.gz ]
then
echo "lzma command not installed"
echo "Switching permanently to gzipped initrd"
sed -i -e 's/initrd\.lz/initrd.gz/g' text.cfg txt.cfg
rm -f ../casper/initrd.lz
else
: do nothing – no initrd.gz
fi
fi
else
: do nothing – initrd.lz not used
fi
fi
Ahora aprendiendo … DFT y FFT
Las transformadas de Fourier discretas, versión general (DFT) y rápida (FFT).
Para ver si puedo resolver problemas en el espacio de Fourier.
¡Los prefactores lían mucho!
De momento, en python llevo hecho esto: una transformación 1D directa e inversa:
import matplotlib.pyplot as plt
import numpy as np
from math import piT=10
N=256
t = np.linspace(0,T,N)
ft= 3 * np.sin(2*pi*3.6*t + 2)+1
fo = np.fft.fft( ft ) / N
fo = np.fft.fftshift(fo)fo[0]
freq = np.fft.fftfreq( N, float(T)/N )
freq = np.fft.fftshift(freq)#plt.plot(freq, sp.real, freq, sp.imag)
plt.plot(freq, abs( fo ) )plt.show()
ft2 = N * np.fft.ifft( fo )
Cálculo de la segunda derivada a través de la transformada, 1D:
import matplotlib.pyplot as plt
import numpy as np
from math import piT=10
N=256
om=0.6t = np.linspace( 0 , T , N , endpoint=False )
ft= 3 * np.sin( 2*pi* om *t + 2)+1
fo0 = np.fft.fft( ft ) / N
fo = np.fft.fftshift( fo0 )fo0[0]
freq0 = np.fft.fftfreq( N, float(T)/N )
q = 2*pi* freq0freq = np.fft.fftshift( freq0 )
ddfo = – q**2 * fo0#plt.plot(freq, sp.real, freq, sp.imag)
plt.plot(freq, abs( fo ) )plt.show()
ft2 = N * np.fft.ifft( fo0 )
ddft = N * np.fft.ifft( ddfo )
Transformada directa e inversa en 2D:
import matplotlib.pyplot as plt
import numpy as np
from math import piL=10
N=64[x, y] = np.meshgrid( np.linspace(0,L,N),
np.linspace(0,L,N))kx=0.2 #2.2
ky=0.7 #1.7f = np.sin( 2*pi* ( kx * x + ky * y ) ) + np.random.uniform(0, 1, x.shape)
# plt.pcolor(x,y,f)
fou0 = np.fft.fft2( f ) / (N*N)
fou = np.fft.fftshift( fou0 )freq = np.fft.fftfreq( N, float(L)/N )
freq = np.fft.fftshift(freq)[fx , fy] = np.meshgrid( freq, freq )
plt.pcolor(fx,fy,abs(fou) )
#plt.plot(freq, sp.real, freq, sp.imag)
#plt.plot(freq, abs( fo ) )plt.show()
f2 = N * N * np.fft.ifft2( fou0 )
plt.pcolor(x,y,f)
plt.pcolor(x+L,y,f2.real)
Ahora aprendiendo … Galerkin projection
Una mezcla bastante explosiva de solución numérica de ecuaciones en derivadas parciales y álgebra lineal.
Ver: The POD method and Galerkin approximations, del Professor Kutz, Applied Mathematics University of Washington in 1990.
Por cierto, en sus vídeos emplea una curiosa técnica, escribiendo mirando al espectador pero al derecho. Como escribe con mano izquierda, yo creo que se trata de una grabación en un espejo
Por cierto, acaba de aparecer de un artículo donde emplean esta técnica, escrito en parte por compañeros de Aeronáuticos.
Numerología
¡Primera entrega sobre numerología!
Por mucho que me guste xkcd, esta vez creo que el chiste no tiene sentido.
El problema, en mi opinión, es que 2:53 no tiene mucho que ver con el número 253.

¿Por qué no?
Cada uno es libre de divertirse como quiera, pero una persona tan formada como Randall Munroe debería darse cuenta de lo siguiente:
- Hay 60 minutos en una hora
- Las horas comienzan desde un origen arbitrario
- No tiene sentido "factorizar" una hora (al menos, cuesta encontrarlo)
Hablaré de todo esto en futuras entregas, pero de momento adelanto mi tesis: nada de un número que tenga como origen una elección arbitraria convencional puede considerarse una propiedad interesante de un número.
Adios a las "horas curiosas" como 2:22.
Y, por supuesto, a las fechas como el 22 del 2. Por no hablar de las 2:22 del 22 del 2 del 2222. No significa nada.
Ojo, una de las convenciones arbitrarias es el propio sistema de numeración en base 10.


Comentarios recientes