Inicio » Matemáticas
Archivos de la categoría: Matemáticas
Diagramas de Voronoi… ¿en todas partes?
Es inevitable: cuando se aprende algo atractivo, uno comienza a verlo en todas partes. El efecto tiene un nombre: Fenómeno Baader-Meinhof, y creo que es más famoso ya el fenómeno que la organización terrorista a la que se refiere.
Las ciencias no son una excepción en este sentido, sobre todo si hablamos de patrones espaciales. Uno de ellos es el diagrama de Voronoi que, para una colección de puntos (“generadores”), asocia a cada uno la zona más cercana.
El asunto con este diagrama es que es fácil construirlo si a uno le dan los puntos generadores:

Lo curioso es que, si a uno ya le dan el diagrama (o algo que se le parece), no es tan fácil encontrar los puntos generadores.
Aquí, un diagrama visto en la piel de una jirafa. Parece de Voronoi, pero ¿lo es? ¿Podemos cuantificar cuánto se desvía? ¿Dónde están los puntos?

Las tres preguntas están relacionadas, por supuesto. Un procedimiento descrito por Hisao Honda en 1978 nos ayuda a encontrar los puntos generadores. Si las semi-rectas descritas se cruzan todas en un punto, el diagrama es de Voronoi. Si no, no lo es, pero aun así él propuso una medida de la desviación de los cruces para cuantificar cómo de “lejos” estaría esta celda en particular de ser parte de un diagrama de Voronoi (en esto no vamos a entrar).
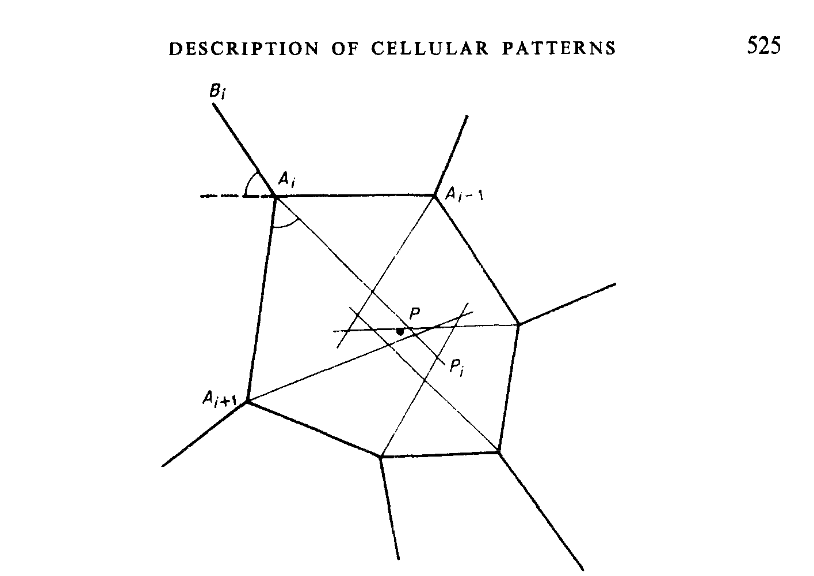
Hisao Honda (1978). Description of cellular patterns by Dirichlet domains: The two-dimensional case. , 72(3), 523–543. doi:10.1016/0022-5193(78)90315-6
Para este tipo de cálculos, está genial geogebra, un programa gratuito de geometría (que, además, permite importar imágenes y dibujar sobre ellas). Si probamos la construcción anterior, comenzando con la intersección D y luego con la C…
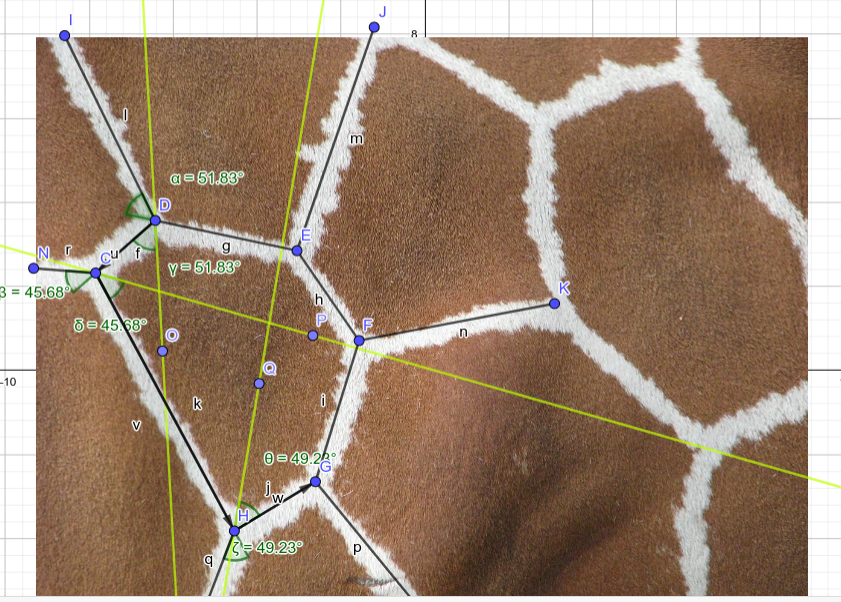
Bueno, el dibujo tiene muchos detalles, pero la idea siempre es tomar un segmento como el DE, ver qué ángulo hace su continuación con el segmento que se va “fuera” de la celda (el DI). En este caso, es de 51.83º. Luego, trazamos una recta desde D que forme este mismo ángulo con el segmento DC. Y así. Al trazar la tercera línea nos damos cuenta de que el diagrama no es NADA de Voronoi!! Si lo fuera, todas las rectas se cortarían en un punto, que es el generador. Por supuesto, esto no va a pasar nunca (aunque sólo sea por errores de perspectiva, de fotografía…), pero sí hay diagramas reales donde el resultado es mucho mejor.

Para el futuro: desmitificar los frecuentes anuncios de hallazgos de diagramas de Voronoi hasta en la sopa (¡literalmente!)
Análisis de estabilidad de von Neumann
Este método es muy conocido para analizar los parámetros en una discretización que garantizan la estabilidad del método numérico. Ver, por ejemplo, el análisis de la ecuación de difusión en wikipedia (que yo, ejem, acabo de modificar). Pero, en mi opinión, la discusión se mete en funciones trigonométricas que despistan bastante. Sobre todo, porque acaban evaluadas en "la peor situación", que se ve venir de antemano. Aquí propongo anticipar esa situación desde el principio.
Por cierto: es "fon no i man"
Ahora aprendiendo … DFT y FFT
Las transformadas de Fourier discretas, versión general (DFT) y rápida (FFT).
Para ver si puedo resolver problemas en el espacio de Fourier.
¡Los prefactores lían mucho!
De momento, en python llevo hecho esto: una transformación 1D directa e inversa:
import matplotlib.pyplot as plt
import numpy as np
from math import piT=10
N=256
t = np.linspace(0,T,N)
ft= 3 * np.sin(2*pi*3.6*t + 2)+1
fo = np.fft.fft( ft ) / N
fo = np.fft.fftshift(fo)fo[0]
freq = np.fft.fftfreq( N, float(T)/N )
freq = np.fft.fftshift(freq)#plt.plot(freq, sp.real, freq, sp.imag)
plt.plot(freq, abs( fo ) )plt.show()
ft2 = N * np.fft.ifft( fo )
Cálculo de la segunda derivada a través de la transformada, 1D:
import matplotlib.pyplot as plt
import numpy as np
from math import piT=10
N=256
om=0.6t = np.linspace( 0 , T , N , endpoint=False )
ft= 3 * np.sin( 2*pi* om *t + 2)+1
fo0 = np.fft.fft( ft ) / N
fo = np.fft.fftshift( fo0 )fo0[0]
freq0 = np.fft.fftfreq( N, float(T)/N )
q = 2*pi* freq0freq = np.fft.fftshift( freq0 )
ddfo = – q**2 * fo0#plt.plot(freq, sp.real, freq, sp.imag)
plt.plot(freq, abs( fo ) )plt.show()
ft2 = N * np.fft.ifft( fo0 )
ddft = N * np.fft.ifft( ddfo )
Transformada directa e inversa en 2D:
import matplotlib.pyplot as plt
import numpy as np
from math import piL=10
N=64[x, y] = np.meshgrid( np.linspace(0,L,N),
np.linspace(0,L,N))kx=0.2 #2.2
ky=0.7 #1.7f = np.sin( 2*pi* ( kx * x + ky * y ) ) + np.random.uniform(0, 1, x.shape)
# plt.pcolor(x,y,f)
fou0 = np.fft.fft2( f ) / (N*N)
fou = np.fft.fftshift( fou0 )freq = np.fft.fftfreq( N, float(L)/N )
freq = np.fft.fftshift(freq)[fx , fy] = np.meshgrid( freq, freq )
plt.pcolor(fx,fy,abs(fou) )
#plt.plot(freq, sp.real, freq, sp.imag)
#plt.plot(freq, abs( fo ) )plt.show()
f2 = N * N * np.fft.ifft2( fou0 )
plt.pcolor(x,y,f)
plt.pcolor(x+L,y,f2.real)
Ahora aprendiendo … Galerkin projection
Una mezcla bastante explosiva de solución numérica de ecuaciones en derivadas parciales y álgebra lineal.
Ver: The POD method and Galerkin approximations, del Professor Kutz, Applied Mathematics University of Washington in 1990.
Por cierto, en sus vídeos emplea una curiosa técnica, escribiendo mirando al espectador pero al derecho. Como escribe con mano izquierda, yo creo que se trata de una grabación en un espejo
Por cierto, acaba de aparecer de un artículo donde emplean esta técnica, escrito en parte por compañeros de Aeronáuticos.

Comentarios recientes