Inicio » 2022
Archivos anuales: 2022
Diagramas de Voronoi… ¿en todas partes?
Es inevitable: cuando se aprende algo atractivo, uno comienza a verlo en todas partes. El efecto tiene un nombre: Fenómeno Baader-Meinhof, y creo que es más famoso ya el fenómeno que la organización terrorista a la que se refiere.
Las ciencias no son una excepción en este sentido, sobre todo si hablamos de patrones espaciales. Uno de ellos es el diagrama de Voronoi que, para una colección de puntos (“generadores”), asocia a cada uno la zona más cercana.
El asunto con este diagrama es que es fácil construirlo si a uno le dan los puntos generadores:

Lo curioso es que, si a uno ya le dan el diagrama (o algo que se le parece), no es tan fácil encontrar los puntos generadores.
Aquí, un diagrama visto en la piel de una jirafa. Parece de Voronoi, pero ¿lo es? ¿Podemos cuantificar cuánto se desvía? ¿Dónde están los puntos?

Las tres preguntas están relacionadas, por supuesto. Un procedimiento descrito por Hisao Honda en 1978 nos ayuda a encontrar los puntos generadores. Si las semi-rectas descritas se cruzan todas en un punto, el diagrama es de Voronoi. Si no, no lo es, pero aun así él propuso una medida de la desviación de los cruces para cuantificar cómo de “lejos” estaría esta celda en particular de ser parte de un diagrama de Voronoi (en esto no vamos a entrar).
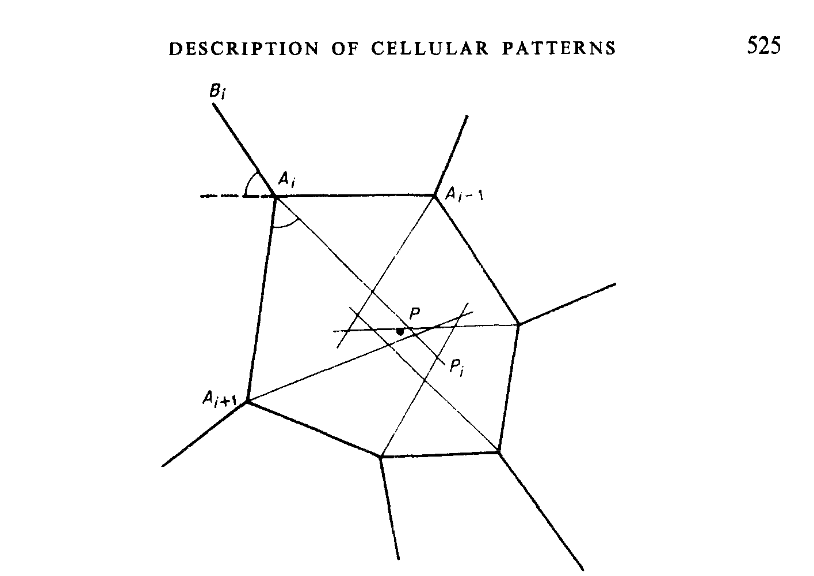
Hisao Honda (1978). Description of cellular patterns by Dirichlet domains: The two-dimensional case. , 72(3), 523–543. doi:10.1016/0022-5193(78)90315-6
Para este tipo de cálculos, está genial geogebra, un programa gratuito de geometría (que, además, permite importar imágenes y dibujar sobre ellas). Si probamos la construcción anterior, comenzando con la intersección D y luego con la C…
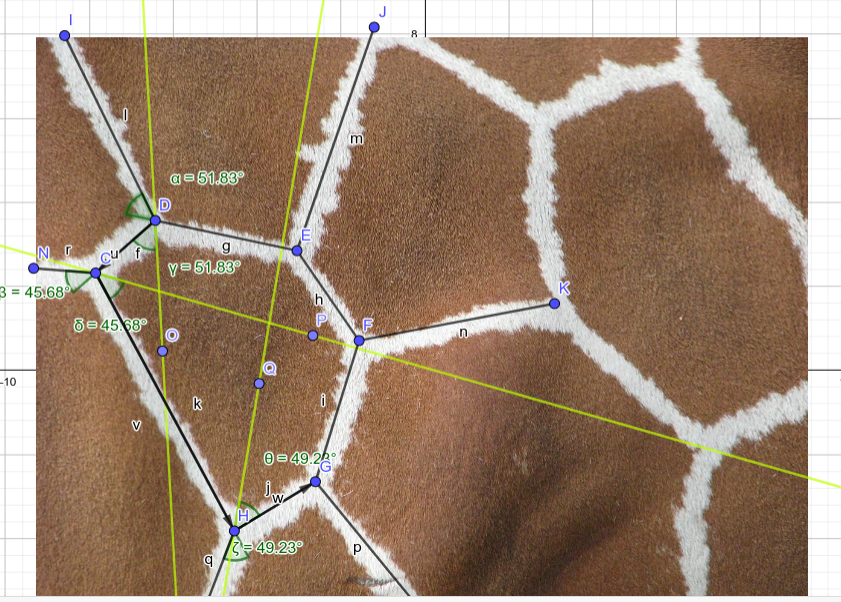
Bueno, el dibujo tiene muchos detalles, pero la idea siempre es tomar un segmento como el DE, ver qué ángulo hace su continuación con el segmento que se va “fuera” de la celda (el DI). En este caso, es de 51.83º. Luego, trazamos una recta desde D que forme este mismo ángulo con el segmento DC. Y así. Al trazar la tercera línea nos damos cuenta de que el diagrama no es NADA de Voronoi!! Si lo fuera, todas las rectas se cortarían en un punto, que es el generador. Por supuesto, esto no va a pasar nunca (aunque sólo sea por errores de perspectiva, de fotografía…), pero sí hay diagramas reales donde el resultado es mucho mejor.

Para el futuro: desmitificar los frecuentes anuncios de hallazgos de diagramas de Voronoi hasta en la sopa (¡literalmente!)
STAR-CCM+ messes up python3 – linux
Just a quick note in case somebody looks this up. Siemens’ Simcenter STAR-CCM+, a fine CFD program, has a funny way of installing itself on linux. It will modify /etc/profile this way
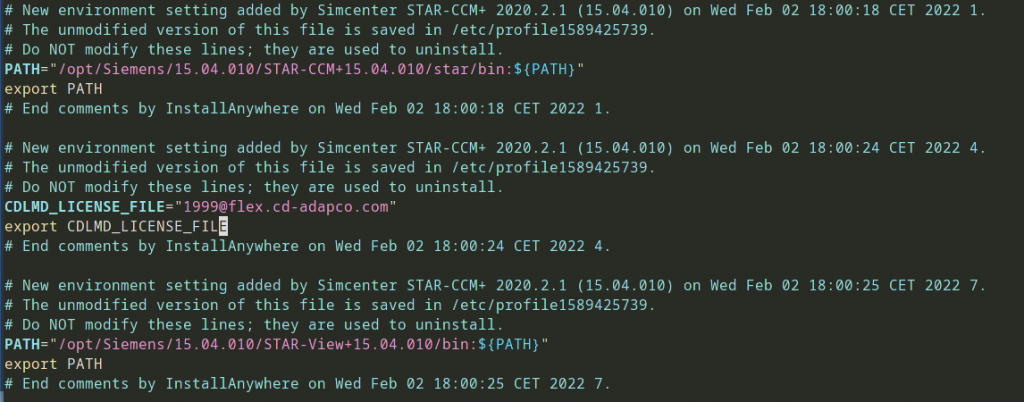
What it does, it changes your PATH so that “python3” now means “/opt/Siemens/15.04.010/STAR-CCM+15.04.010/star/bin/python3” (run which python3 to check this). (The actual version number may change on your system, of course.)
Also, notice /opt/Siemens/15.04.010/STAR-CCM+15.04.010/star/bin/python3 gets added TWICE to the PATH variable. That’s because I installed two times… it may appear many times, I guess. That would mean that “uninstall” does not work as well.
So, I would suggest eliminating those sections, even if uninstall may complain in the future, and creating a new small script with them, that should be run when STAR-CCM+ is needed. All that, as admin, of course.
Otherwise, many python3 applications may not work (it happened with me with calibre, for example).
Or, just comment out those block, and remember to uncomment them when you need to run STAR-CCM+. That’s dirty, but ok as long as you don’t use it too often.
Actualización. ¡It was also messing my installation of aquagpusph ! A more elegant way is simple to reverse the path-altering command:
PATH="${PATH}:/opt/Siemens/15.04.008/STAR-CCM+15.04.008/star/bin"
instead of
PATH="/opt/Siemens/15.04.008/STAR-CCM+15.04.008/star/bin:${PATH}"
The Maxwell and common tangent constructions
In some theories, the energy is predicted to have this funny shape. The concave region is not allowed, so the simplest idea is just to fill the region with a segment (to form a “convex hull”). This is called the common tangent construction, and it is related to very classic Maxwell construction. Originally, JC Maxwell used this construction when analyzing results from the van der Waals equation of state for fluids.
The wikipedia article on Maxwell construction is fine, but the related common tangent construction does not exist! (you can create it if you feel like it). I have therefore written down these notes with information about this construction. Very simple, really, but my thermodynamics was very rusty!


Comentarios recientes