Los lenguajes de programación más solicitados en 2021
La programación de ordenadores sigue siendo un campo con interesantes salidas laborales. Esto es especialmente cierto en el campo de la Ingeniería Civil, por tratarse de un sector consumidor de muchos recursos informáticos. Actualmente existen más de 700 lenguajes de programación activos. Este artículo hablará sobre los lenguajes más demandados en el año 2021, según distintas fuentes.
Con la excepción de los lenguajes dedicados a la programación de bases de datos, la mayoría de los índices miden la importancia de los lenguajes en su uso general, no dentro de un campo específico. Es por ello, que los lenguajes cuya utilización se da principalmente dentro de un campo concreto, salen penalizados, y su posición en los índices generales no muestra realmente su posición si se considerara solo su prevalencia en dicho campo.
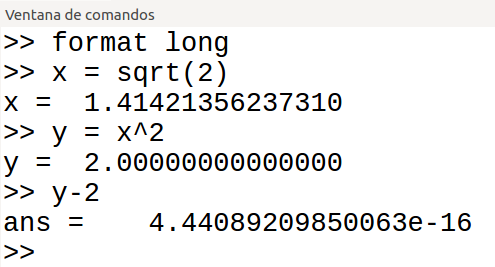
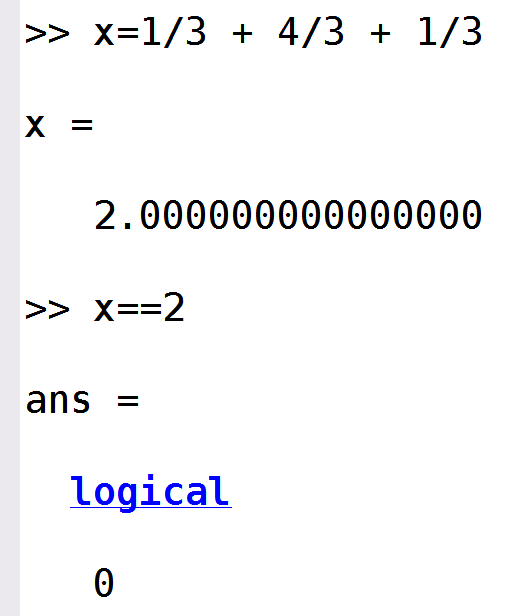
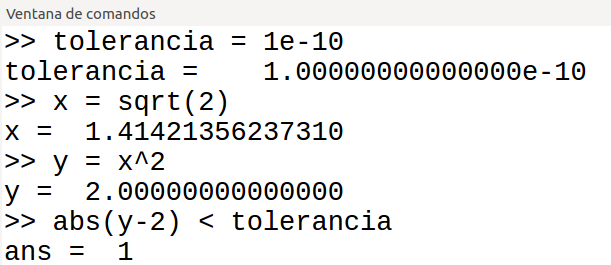
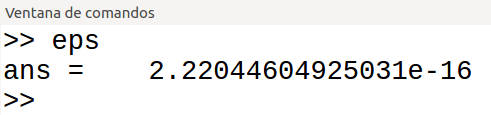
Es el caso de MATLAB-Octave, cuyo uso está restringido al ámbito científico. Uno de los índices más prestigiosos es el índice TIOBE, basado en las búsquedas en internet referentes a los diferentes lenguajes. El índice TIOBE del mes de octubre de 2021 indica que MATLAB ocupa la posición 13 entre los lenguajes más utilizados. Esto supone un incremento de uso respecto de octubre de 2020, cuando ocupaba la posición 15.
En todos los índices, las primeras posiciones están copadas por Python, Java y las diferentes variantes del C: C, C++ y C#. Son sin duda los lenguajes más utilizados para programación general. Java, que venía siendo el más utilizado durante muchos años, ha cedido la primera posición en favor de Python y C. Cualquiera de ellos es una buena opción para profundizar en la programación. Si nos limitamos al ámbito científico, tal vez Python ofrece, a día de hoy, una combinación de recursos y facilidad de uso que lo convierten en la opción más atractiva.
Es significativa la evolución del lenguaje Fortran. Hace muchos años era el lenguaje científico por excelencia. De hecho, era el lenguaje que se estudiaba en la Escuela de Caminos allá por los años 80 y 90 del siglo pasado. Más tarde, Fortran perdió importancia y pasó a ser un lenguaje muy minoritario. Las mejoras aportadas en las útimas versiones, junto con su rapidez de ejecución y su enfoque científico han hecho que vuelva a ser un lenguaje muy utilizado. En el citado índice TIOBE de octubre de 2021, ocupa la posición 18 entre los lenguajes más utilizados, ascendiendo a esta posición desde la posición 37 que ocupaba el año pasado.
En el último artículo que dediqué a los lenguajes más utilizados, hablaba de Rust y Go. Los sigo considerando dos lenguajes muy interesantes y con mucho futuro. En el índice TIOBE de octubre 2021, Go ocupa la posición 12 y Rust la 26. Son lenguajes fundamentalmente dedicados a la programación de sistemas. Como opción laboral, son de los que mejores sueldos ofrecen a los programadores. Les seguiremos la pista para ver su evolución. Seguro que seguirán dando que hablar en el futuro.
Es muy interesante la encuesta anual de Stack Overflow, que ofrece respuestas a numerosas preguntas acerca del perfil de los lenguajes de programación y de los propios programadores.
A continuación se ofrece una lista de enlaces a algunos índices y a artículos comentando los distintos índices:
Stack Overflow Developer Survey 2021TIOBE Index
The most in-demand programming languages of 2021 by TNW
Most in Demand Programming Languages 2021 by Merehead
GitHub Top Programming Languages
Top Programming Languages 2021 by IEEE Spectrum