La proyección cartográfica es una correspondencia entre los puntos de la superficie terrestre y sus transformados en el plano llamado plano de proyección, para ello se establece una radiación de semirrectas a través de un punto denominado vértice de proyección, para establecer una correspondencia entre los puntos de la superficie terrestre y sus transformados en el plano llamado plano de proyección. El método para efectuar esta correspondencia consiste en generar un conjunto de semirrectas a través del punto denominado vértice de proyección a fin de obtener una correspondencia entre cada punto de intercepción en la esfera y su homólogo en el plano cortado por la misma semirrecta.
Debido a ciertas distorsiones afectan a las proyecciones de cuerdo a como se proyecten, estas distorsiones pueden afectar al área, las distancias o los ángulos de los elementos representados por lo que resulta muy importante decidir que proyección se va a emplear para minimizar las distorsiones. Dependiendo de sus fundamentos, características y propiedades las proyecciones cartográficas se clasifican de la siguiente manera:
EN FUNCIÓN DE SUS CUALIDADES MÉTRICAS
Como al pasar de la esfera al plano resulta imposible conservar las propiedades geométricas como los ángulos, además de que las superficies y distancias se verán distorsionadas, las proyecciones cartográficas se pueden clasificar de acuerdo a la cualidad que conserve en:
Una proyección cartográfica es conforme cuando mantiene los ángulos que forman dos líneas en la superficie terrestre, este tipo de proyección se usa en cartas de navegación.
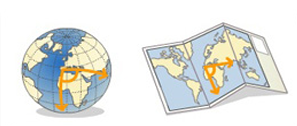
Imagen de la IGN en Conceptos Cartográficos
Una proyección cartográfica es equivalente cuando en el mapa se conservan las superficies del terreno, aunque las figuras deben ser semejantes, se usan generalmente en mapas temáticos o parcelarios.
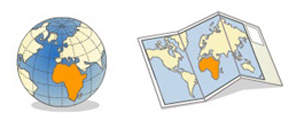
Imagen de la IGN en Conceptos Cartográficos
Una proyección cartográfica es equidistante cuando mantiene las distancias entre dos puntos situados en la superficie terrestre, esta distancia está representada por el arco de circulo máximo que los une.
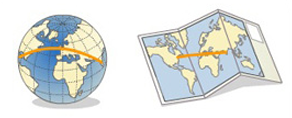
Imagen de la IGN en Conceptos Cartográficos
Una proyección cartográfica es afiláctica cuando no conserva ángulos, superficies ni distancias, pero las deformaciones son mínimas.
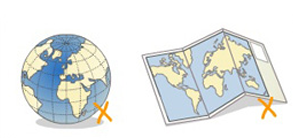
Imagen de la IGN en Conceptos Cartográficos
EN FUNCIÓN DE SUS CUALIDADES PROYECTIVAS
Las proyecciones se pueden clasificar en función de la figura sobre la cual se proyecta, esto es, las que utilizan el plano o las que se desarrollan a través de una figura geométrica (cono o cilindro).
Perspectivas o planas.
Estas se obtienen proyectando la superficie terrestre desde un punto llamado vértice de proyección sobre un plano tangente sobre a un punto de la Tierra llamado centro de proyección. La proyección mantiene sus propiedades geométricas alrededor del centro de proyección y las distorsiones aumentan conforme nos alejamos de dicho punto. El punto considerado como vértice de proyección puede encontrarse en el exterior, sobre la superficie o en el interior de la esfera y el punto de tangencial puede ser cualquier punto de su superficie. En consecuencia, la proyección plana permite dos clasificaciones en función del vértice respecto a la esfera y en función de la posición el paño tangente a la esfera.
Según la posición del vértice respecto de la esfera:
El punto considerado como vértice y proyección puede encontrarse en el interior, sobre la superficie o en el exterior de la esfera.
En este tipo de proyecciones el vértice coincide con el centro de la figura esférica que representa la Tierra, por lo tanto, no es posible todo un hemisferio. Los círculos máximos (meridianos, ecuador y ortodrómicas) se representan como rectas y al alejarse del centro de proyección hay grandes distorsiones.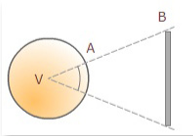
Imagen de la IGN en Conceptos Cartográficos
Se emplea en cartas de navegación aérea y marítima y para representar las zonas polares.
En este caso el vértice de proyección está situado sobre la superficie de la esfera y su punto diametralmente opuesto es el punto de tangencia el plano de proyección. La deformación aumenta simétricamente hacia el exterior a partir del punto central, mientras que meridianos y paralelos se representan como circunferencias. 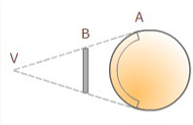
Imagen de la IGN en Conceptos Cartográficos
La proyección estereográfica es adecuada para representar la totalidad de un hemisferio, por lo que se utiliza en la representación de las zonas polares, mapamundis, mapas de estrellas y geofísicos.
En este tipo de proyecciones el vértice de proyección se encuentra a una distancia infinita de la esfera terrestre. La escala se conserva sólo en el centro, mientras que la deformación aumenta rápidamente al alejarse de este punto. Es un tipo de proyección muy antigua que solo s rusa para la realización de cartas astronómicas y para representar la apariencia de la Tierra desde el espacio
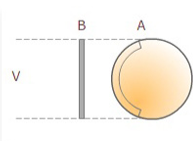
Imagen de la IGN en Conceptos Cartográficos
El vértice de proyección es un punto cualquiera del espacio exterior a la esfera, pero a una distancia finita de su centro y su punto de tangencia puede ser cualquier punto de la superficie de la esfera.

Imagen de la IGN en Conceptos Cartográficos
Las proyecciones escenográficas se destinan a la realización de mapas celestes.
Según posición del plano tangente a la esfera
El punto de tangencia puede ser cualquier punto de la superficie de la esfera.
Las proyecciones polares también reciben el nombre de ecuatoriales, por ser su plano
paralelo el del ecuador y por lo tanto, perpendicular al eje de la Tierra.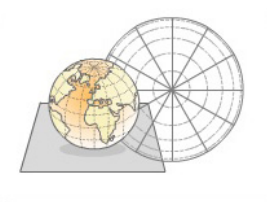
Imagen de la IGN en Conceptos Cartográficos
Los meridianos se representan por rectas concurrentes al centro de proyección,
localizado en cualquiera de los polos y conservando el valor de sus ángulos. En
consecuencia, la escala de representación varía con la latitud.
Las proyecciones meridianas o transversas al ser el punto de tangencia el punto de corte
de cualquier meridiano con el ecuador.
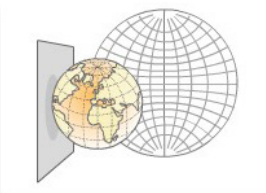
Imagen de la IGN en Conceptos Cartográficos
En este tipo de proyecciones los paralelos y meridianos se representan mediante curvas
transcendentes. En el caso de la proyección gnomónica meridiana (centro de proyección
coincidente con el centro de la Tierra)los meridianos se representan por rectas paralelas
entre sí, desigualmente espaciadas, mientras que los paralelos se representan por
hipérbolas.
Las proyecciones oblicuas se denominan también horizontales por ser paralelas al
horizonte de un lugar. El punto de tangencia está situado en un punto cualquiera que no
se encuentre en el ecuador ni en ninguno de los polos.
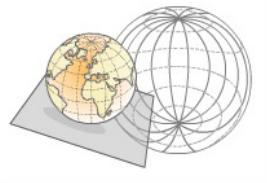
Imagen de la IGN en Conceptos Cartográficos
En este proyección los paralelos quedan representados como curvas cónicas tales como
parábolas, elipses e hipérbolas.
Desarrollos
Este tipo de proyección se obtiene al considerar una figura geométrica auxiliar tangente o secante a la esfera que pueda convertirse después en un plano, es decir que sea desarrollable. Las figuras auxiliares más utilizadas son el cono y el cilindro, por lo que tenemos las siguientes proyecciones:
Proyecciones cónicas
Emplean el cono como figura de proyección, tangente o secante a la esfera. El eje del cono coincide con la línea de los polos, estableciendo una correspondencia entre los puntos de la esfera y el cono.
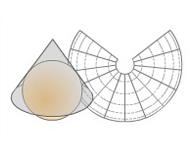
Imagen de la IGN en Conceptos Cartográficos
Al desarrollar el cono se obtiene una representación en la que los meridianos aparecen como rectas concurrentes al vértice del cono y forman ángulos iguales entre sí, mientras que los paralelos son circunferencias concéntricas cuyo centro es el vértice del cono, como por ejemplo las proyecciones de Lambert y Bonne.
Proyecciones cilíndricas
Utilizan el cilindro como figura de proyección, tangente o secante a la esfera. El eje del cilindro coincide con la línea de los polos, estableciendo una correspondencia entre los puntos de la esfera y el cilindro. 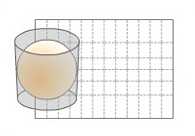
Imagen de la IGN en Conceptos Cartográficos
Cuando se desarrolla el cilindro se obtiene una representación en la que los meridianos estarán representados por rectas paralelas equidistantes y los paralelos por rectas perpendiculares a las anteriores que se van espaciando a medida que aumenta la latitud, ejemplo de esta proyección son la Mercator y la UTM (Universal Transversa de Mercator).
PROYECCIONES MODIFICADAS
Son las diseñadas para poder representar la totalidad de la superficie terrestre sin incurrir en deformaciones excesivas a fin de representar fenómenos geográficos globales.
Algunos ejemplos de este tipo de proyección son los siguientes:
Los paralelos son rectas horizontales equidistantes, el meridiano central es una recta perpendicular a ellas y los restantes meridianos son curvas. En esta proyección sólo son verdaderas las distancias a lo largo de todas las latitudes y el meridiano central. Es una proyección equivalente porque conserva las áreas.
Se emplea para representaciones donde las relaciones donde las relaciones de latitud son significativas al estar los paralelos uniformemente espaciados. 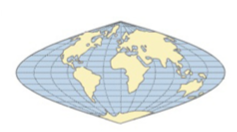
Imagen de la IGN en Conceptos Cartográficos
El ecuador tiene doble longitud que el meridiano central y está dividido en partes iguales que marcan los pasos de los meridianos, que quedan representados por elipses. Los paralelos se representan por rectas horizontales paralelas al ecuador y su separación queda determinada por la condición de que las áreas de las franjas entre paralelos sean semejantes en la superficie terrestre. Por ello esta proyección es equivalente, es decir conserva las áreas.
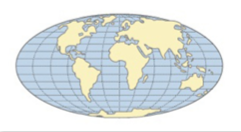
Imagen de la IGN en Conceptos Cartográficos
Es utilizada para distribuciones mundiales cuando el interés se concentra en latitudes medias.
Es una proyección discontinua. En la que la Tierra se representa en partes irregulares unidas, de esta forma se mantiene la sensación d esfera y se consigue una distorsión mínima de las zonas continentales, pero con huecos en las superficies oceánica.
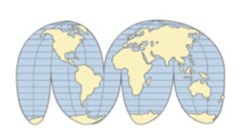
Imagen de la IGN en Conceptos Cartográficos
Es útil para la representación de datos en el mundo una que su área es igual a la real. Se utiliza en los mapas de distribución de productos.