Procesado Avanzado de Señales y Datos

Otro sitio más de UPM [Blogs]

Curso 2022/23

INFERENCIA APROXIMADA Y REDES BAYESIANAS

eraymond

Iñigo García-Vallaure Martín, Laura Alejandra Noreña Blandon y Eric Antonio Raymond Rodrigues

INTRODUCCIÓN

A través de este blog vamos a observar las distintas utilidades de la inferencia aproximada y de las redes bayesianas. Se tratan de dos aplicaciones fundamentales en el ámbito del aprendizaje automático y en el campo de la inteligencia artificial, apoyándose en métodos probabilísticos y en la toma de decisiones basadas en la incertidumbre.

El objetivo de la inferencia aproximada es estimar la distribución de probabilidad de variables que no son conocidas a través de observaciones, ya que computacionalmente puede resultar costoso. Es útil en problemas donde las relaciones entre variables son difíciles de ajustar de forma exacta.

Por su parte, las redes bayesianas son modelos probabilísticos que relacionan variables mediante grafos acíclicos dirigidos. Los nodos representan las variables, las cuales están relacionadas entre ellas de manera dependiente o independiente. Una vez desarrollado el modelo, en base a nuevas evidencias, podemos obtener la probabilidad a posteriori del conjunto de variables. Las aristas que unen los nodos representan las dependencias probabilísticas entre las variables.

Si combinásemos estas dos aplicaciones, podría ser bastante provechoso en distintos ámbitos, como la robótica, medicina, ingeniería o en la toma de decisiones.

En resumen, la inferencia aproximada y las redes bayesianas con herramientas fundamentales para lidiar con la incertidumbre en problemas complejos de inferencia probabilística, ya que sería efectivo a la hora de resolver problemas del mundo real.

ESTADO DEL ARTE

En los últimos años, los campos de la inferencia aproximada y las redes bayesianas han padecido grandes avances. Ambos se centran en realizar inferencias eficientes y precisas en modelos probabilísticos.

La inferencia aproximada, en vez de calcular la distribución posterior exacta (la cual es computacionalmente costosa), busca encontrar una aproximación cercana a través de métodos más eficientes. Algunos de los mencionados métodos son la inferencia variacional: se plantea la inferencia como un problema de optimización donde se busca encontrar una distribución lo más semejante posible a la distribución posterior real; la aproximación de Monte Carlo: emplea distintos procedimientos que utilizan muestras aleatorias para aproximar la distribución posterior. Algunas de las técnicas manejadas son el muestreo de Gibbs, el muestreo de Importancia o el Muestreo de Aceptación y Rechazo; y la aproximación determinista: se aproxima a la distribución posterior mediante técnicas deterministas como la cuadratura de Gauss o la factorización de momentos.

Por su lado, las redes bayesianas son necesarias para modelar incertidumbre y realizar inferencias basadas en reglas de probabilidad. Han ayudado al desarrollo y progreso de redes bayesianas profundas: gracias a la unión de las redes bayesianas con arquitecturas profundas, como por ejemplo, las redes neuronales, han aparecido redes bayesianas profundas, las cuales permiten modelar incertidumbre en las predicciones y proporcionan una forma más robusta de aprendizaje automático; de la inferencia aproximada en redes bayesianas: la inferencia aproximada es bastante importante en las redes bayesianas, sobre todo cuando el número de variables es muy alto o la estructura del modelo es compleja. Los avances en técnicas de inferencia aproximada han mejorado la eficiencia y la precisión de las inferencias realizadas en redes bayesianas; y del aprendizaje estructural: se han llevado a cabo y desarrollado algoritmos más eficientes para estudiar la estructura de las redes bayesianas a partir de datos observados. Con estos algoritmos, se pueden descubrir automáticamente las relaciones de dependencia entre las variables y construir modelos más precisos.

El problema de inferencia en una red bayesiana es un problema NP- completo en redes grandes. Debido a esto, para resolverlo se han propuesto alternativas exactas y aproximadas, las cuales pueden ser determinísticos o estocásticos. Los algoritmos determinísticos intentan simplificar el problema de alguna manera, como por ejemplo, con la eliminación de nodos (se seleccionan nodos para realizar los cálculos necesarios y se eliminan los demás) o con la eliminación de arcos (donde se eliminan todos aquellos arcos que codifican relaciones detectadas como “débiles”). Los algoritmos estocásticos se basan en realizar determinadas simulaciones a partir de una distribución de probabilidad existente en la red y, así, estimar la probabilidad de interés.

DESARROLLO

Las redes bayesianas son modelos probabilísticos que representan relaciones causales entre variables utilizando grafos dirigidos acíclicos. Estas redes se basan en el teorema de Bayes y son utilizadas para modelar la incertidumbre y realizar inferencias probabilísticas.
El desarrollo de una red bayesiana generalmente implica los siguientes pasos:

  1. Identificar las variables relevantes: comienza por identificar las variables que deseas modelar en tu problema. Estas variables pueden ser discretas o continuas y representar diferentes aspectos del sistema que estás estudiando.
  2. Definir la estructura del grafo: una vez que hayas identificado las variables, debes definir la estructura del grafo dirigido acíclico que representará las relaciones causales entre ellas. Esto implica determinar qué variables dependen directamente de otras variables.
  3. Especificar las distribuciones de probabilidad condicional: para cada variable en la red, se deben de especificar su distribución de probabilidad condicional (DPC) dado el estado de sus variables padre. Esto implica determinar la probabilidad de cada posible estado de una variable dada la combinación de estados de sus variables padre.
  4. Estimar los parámetros de la red: una vez que se hayan especificado las DPCs, es necesario estimar los parámetros de la red a partir de datos observados. Esto puede implicar el uso de técnicas como el método de máxima verosimilitud o el enfoque bayesiano.
  5. Realizar inferencias: una vez que la red bayesiana está desarrollada y los parámetros están estimados, la utilizamos para realizar inferencias probabilísticas. Esto implica responder preguntas sobre la probabilidad de ciertos estados de las variables dadas ciertos valores observados o evidencia.
    Es importante destacar que desarrollar una red bayesiana puede ser un proceso iterativo, en el cual puedes ajustar y refinar la estructura del grafo y las DPCs a medida que adquieres más conocimiento y datos. Además, existen diversas herramientas y bibliotecas que pueden facilitar el desarrollo y la manipulación de redes bayesianas, como PyMC3, Stan, y la librería bnlearn en R.

Ejemplo básico de red bayesiana:
Supongamos que tenemos las siguientes variables:

  1. “Cáncer de mama”: Variable que indica si el paciente tiene cáncer de mama o no. Puede tomar los valores “Sí” o “No”.
  2. “Resultado de la mamografía”: Variable que indica el resultado de la mamografía del paciente. Puede tomar los valores “Negativo” o “Positivo”.
  3. “Edad”: Variable que indica la edad del paciente. Puede tomar los valores “Joven”, “Media” o “Mayor”.
  4. “Historial familiar”: Variable que indica si el paciente tiene antecedentes familiares de cáncer de mama. Puede tomar los valores “Sí” o “No”.
    La estructura de la red bayesiana para este ejemplo se muestra de la siguiente manera:

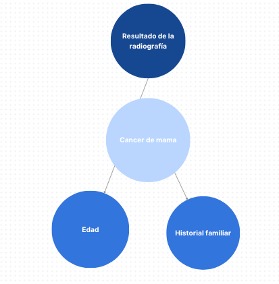
En este ejemplo, asumimos que el resultado de la mamografía influye en la probabilidad de tener cáncer de mama, y tanto la edad como el historial familiar también influyen en la probabilidad de tener cáncer de mama.
Para desarrollar esta red bayesiana, necesitaríamos definir las distribuciones de probabilidad condicional para cada variable. Por ejemplo:

  1. P(Cáncer de mama = Sí) = 0.01 (1% de probabilidad de tener cáncer de mama sin tener en cuenta otras variables).
  2. P(Resultado de la mamografía = Positivo | Cáncer de mama = Sí) = 0.8 (80% de probabilidad de obtener un resultado positivo en la mamografía si se tiene cáncer de mama).
  3. P(Resultado de la mamografía = Positivo | Cáncer de mama = No) = 0.1 (10% de probabilidad de obtener un resultado positivo en la mamografía si no se tiene cáncer de mama).
  4. P(Edad = Joven) = 0.3 (30% de probabilidad de ser joven).
  5. P(Edad = Media) = 0.5 (50% de probabilidad de ser de mediana edad).
  6. P(Edad = Mayor) = 0.2 (20% de probabilidad de ser mayor).
  7. P(Historial familiar = Sí | Cáncer de mama = Sí) = 0.6 (60% de probabilidad de tener antecedentes familiares de cáncer de mama si se tiene cáncer de mama).
  8. P(Historial familiar = Sí | Cáncer de mama = No) = 0.1 (10% de probabilidad de tener antecedentes familiares de cáncer de mama si no se tiene cáncer de mama).
    Con estas distribuciones de probabilidad condicional definidas, podemos realizar inferencias probabilísticas sobre la probabilidad de que un paciente tenga cáncer de mama dadas las observaciones de otras variables, como el resultado de la mamografía, la edad y el historial familiar.

RED BAYESIANA IMPLEMENTADA


Se realiza un script en Python para implementar un modelo bayesiano que representa un sistema de diagnóstico médico basado en síntomas y resultados de pruebas médicas. El modelo utiliza una red bayesiana para modelar las relaciones causales entre las variables involucradas:

Las variables en el modelo son las siguientes:

  1. Fiebre: representa la presencia o ausencia de fiebre en el paciente.
  2. Tos: representa la presencia o ausencia de tos en el paciente.
  3. Dolor de garganta: representa la presencia o ausencia de dolor de garganta en el paciente.
  4. Resultado del análisis de sangre: representa el resultado del análisis de sangre del paciente.
  5. Resultado de la radiografía de tórax: representa el resultado de la radiografía de tórax del paciente.
  6. Probabilidad de tener la enfermedad: representa la probabilidad de que el paciente tenga la enfermedad en cuestión.
  7. Diagnóstico final: Representa el diagnóstico final del paciente.
  8. Probabilidad de tener otras enfermedades: representa la probabilidad de que el paciente tenga otras enfermedades
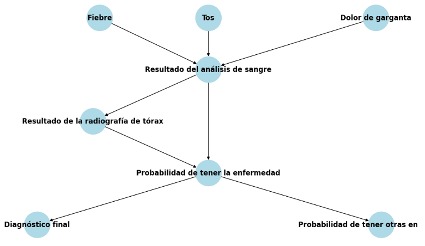
    Las relaciones entre las variables se establecen mediante las aristas en el grafo de la red bayesiana. Por ejemplo, se establece que Fiebre, Tos y Dolor de garganta influyen en el Resultado del análisis de sangre, y este último influye en la Probabilidad de tener la enfermedad y en el Resultado de la radiografía de tórax. A su vez, la Probabilidad de tener la enfermedad influye en el Diagnóstico final y en la Probabilidad de tener otras enfermedades.
    Las distribuciones de probabilidad condicional (CPDs) se definen para cada variable en función de sus padres en el grafo. Estas CPDs especifican cómo las variables padre afectan la probabilidad de los valores de las variables hijas.

MATERIALES

Para el desarrollo correcto de este modelo que implementa la red bayesiana se utilizaron las siguientes librerías de Python:

  1. pgmpy: para modelado y análisis de redes bayesianas y modelos gráficos probabilísticos. Proporciona clases y métodos para construir y manipular redes bayesianas, calcular inferencias probabilísticas y realizar operaciones en los modelos gráficos. En este script, se utiliza para construir el modelo bayesiano, definir las CPDs y realizar inferencias.
  2. networkx: para la creación, manipulación y estudio de estructuras de grafo. Proporciona una implementación de grafo flexible y eficiente, junto con algoritmos para recorrer y analizar los grafos. En este script, se utiliza para visualizar el grafo del modelo bayesiano.
  3. pygraphviz: para la creación y manipulación de gráficos basados en Graphviz. Proporciona una interfaz de Python para trabajar con las funciones y características de Graphviz. En este script, se utiliza junto con networkx para definir el diseño del grafo del modelo bayesiano.

Estas librerías son ampliamente utilizadas en el campo del aprendizaje automático y la inteligencia artificial para modelar y analizar problemas probabilísticos, así como para visualizar y comunicar estructuras de datos complejas como las redes bayesianas.

RESULTADOS

La presencia de fiebre tiene una influencia significativa en la probabilidad de tener la enfermedad. Al observar que una persona presenta fiebre, la probabilidad de tener la enfermedad aumenta considerablemente. Por otro lado, al no presentar fiebre, la probabilidad de tener la enfermedad disminuye significativamente.

Esto sugiere que la fiebre es un factor clave en la detección y diagnóstico de la enfermedad en cuestión. La relación positiva entre la fiebre y la probabilidad de tener la enfermedad puede indicar que la fiebre es un síntoma característico o un indicador temprano de la enfermedad en el modelo.

En resumen, la presencia de fiebre tiene un impacto significativo en la probabilidad de tener la enfermedad según el modelo bayesiano. Esto destaca la importancia de considerar la fiebre como un síntoma relevante al evaluar el riesgo de tener la enfermedad y al tomar decisiones clínicas relacionadas con su diagnóstico y tratamiento.

La presencia de la enfermedad aumenta considerablemente la probabilidad de tener otras enfermedades. Cuando se observa que una persona tiene la enfermedad, la probabilidad de tener otras enfermedades es alta, con un valor de 0.8.

Por otro lado, cuando no se tiene la enfermedad, la probabilidad de tener otras enfermedades disminuye significativamente a 0.2. Esto sugiere que la presencia de la enfermedad está asociada con un mayor riesgo de tener múltiples enfermedades simultáneamente.

Esta inferencia puede tener implicaciones importantes en el ámbito médico. La detección temprana de la enfermedad puede ser un factor crucial para identificar y abordar la presencia de otras enfermedades comórbidas. Por lo tanto, es fundamental considerar la posibilidad de enfermedades adicionales al diagnosticar y tratar a los pacientes con la enfermedad en cuestión.

En resumen, el modelo bayesiano muestra una relación significativa entre la presencia de la enfermedad y la probabilidad de tener otras enfermedades. La detección temprana y el manejo integral de las comorbilidades pueden ser aspectos clave en la atención médica de los pacientes con la enfermedad en cuestión.

DISCUSIÓN

Se pueden sugerir algunas mejoras o áreas de enfoque para mejorar la precisión y utilidad del modelo. Mejorar el modelo bayesiano considerando la inclusión de más variables relevantes, obtener datos más precisos, validar y ajustar el modelo, refinar las distribuciones de probabilidad condicional y considerar la incertidumbre y la sensibilidad en las predicciones. Estas mejoras pueden contribuir a un modelo más preciso y útil para la detección y el manejo de la enfermedad en cuestión.

Mientras que la veracidad de los resultados obtenidos con este modelo bayesiano depende de varios factores como: si el modelo ha sido desarrollado y validado correctamente utilizando datos confiables y representativos, y si se han tenido en cuenta las suposiciones y limitaciones del modelo, los resultados obtenidos pueden ser considerados como una aproximación razonable de la realidad. Sin embargo, es importante recordar que ningún modelo es perfecto y siempre existe cierto grado de incertidumbre asociado a las predicciones realizadas. Por lo tanto, es fundamental interpretar los resultados con precaución y considerarlos como una herramienta complementaria para la toma de decisiones, en lugar de una verdad absoluta.

Finalmente, una red bayesiana es una herramienta muy útil para este tipo de aplicación descrita en el script. Una red bayesiana permite modelar de manera explícita las relaciones probabilísticas entre las variables relevantes en un dominio específico, lo que facilita el razonamiento y la toma de decisiones basados en la incertidumbre.
En el contexto de la aplicación descrita, la red bayesiana permite modelar las relaciones entre los síntomas (fiebre, tos, dolor de garganta), los resultados de los análisis médicos, las probabilidades de tener la enfermedad y otras enfermedades, y el diagnóstico final. Esto proporciona un marco estructurado para representar y analizar la información disponible y realizar inferencias sobre la probabilidad de tener la enfermedad.
La red bayesiana permite combinar de manera coherente la evidencia observada (por ejemplo, la presencia de fiebre) con las probabilidades condicionales y las relaciones causales en el modelo para calcular las probabilidades posteriores de interés, como la probabilidad de tener la enfermedad.
Además, la visualización gráfica de la red bayesiana facilita la comprensión de las relaciones entre las variables y la comunicación de los resultados a diferentes partes interesadas, como médicos, investigadores o pacientes.
Si se construye y valida correctamente, una red bayesiana puede ser una herramienta poderosa para el diagnóstico y la toma de decisiones en el ámbito médico, ya que permite cuantificar y utilizar de manera explícita la información incierta y probabilística disponible. Sin embargo, es importante tener en cuenta las limitaciones y suposiciones del modelo, así como la calidad de los datos utilizados, para interpretar adecuadamente los resultados y tomar decisiones informadas.

BIBLIOGRAFÍA

About