En geometría métrica hay dos conceptos de medida sobre los que se basa su modelo axiomático:

medidas lineales y medidas angulares.

La medida lineal se apoya en el teorema de Pitágoras, y la relación entre este tipo de medidas en el teorema de Thales.

La medida angular la expresamos a partir de relaciones sobre una circunferencia y junto a las anteriores permiten describir la magnitud de las figuras geométricas.

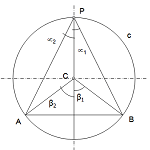
• Ángulo Central -. Es aquel que tiene su vértice en el centro en la circunferencia y tiene por medida el arco comprendido.
• Ángulo inscrito -. es aquel que tiene su vértice en la circunferencia y sus lados son cuerdas.

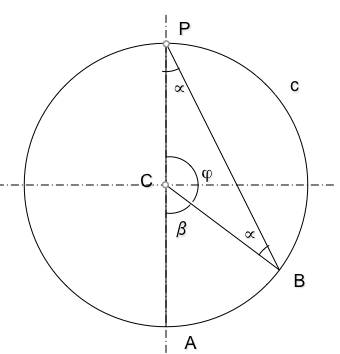
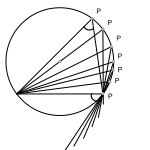
Un ángulo inscrito mide la mitad del ángulo central que abarca el mismo arco.

La suma de ángulos internos de un triángulo es igual a dos rectos, por lo que en el triángulo CBP, que es isósceles (dos ángulos iguales) se cumplirá la relación:

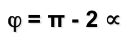
Por lo que tendremos que

Y como consecuencia deduciremos que el ángulo central es el doble que el inscrito

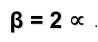
Es fácil generalizar este concepto para posiciones del punto P que no sean tan particulares, ya que podemos descomponer el ángulo en dos y aplicar el mismo razonamiento.

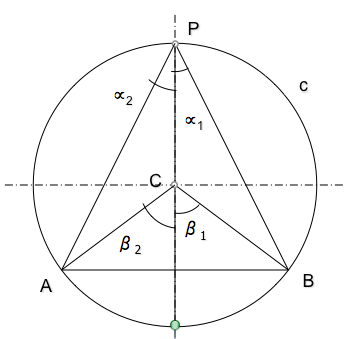
Por ejemplo, si desplazamos el punto P a lo largo de la circunferencia, el ángulo central será la suma de los dos ángulos centrales en que se puede descomponer, siendo por tanto indiferente la posición del punto P.

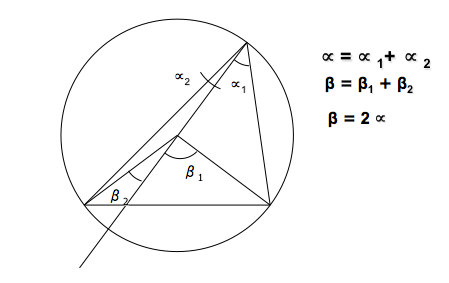
Ejercicios

Los elementos geométricos en el plano que se cortan, rectas y circunferencias, pueden caracterizar su intersección mediante un valor denominado ángulo.

La noción de ángulo entre dos rectas es la más elemental entre las que se dan entre rectas y circunferencias.

A partir de la definición elemental del ángulo entre dos rectas, podremos definir el ángulo formado entre una recta y una circunferencia o el que forman dos circunferencias coplanarias.

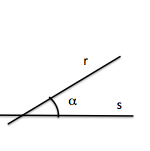
Para definir el concepto de ángulo, previamente, debemos recordar que una recta r divide a un plano en dos semiplanos.

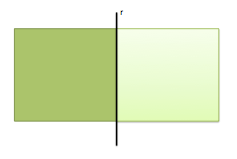
La recta r, tal y como se aprecia en la imagen anterior, divide al plano en dos semiplanos iguales. El área de cada uno de estos semiplanos no es medible. Podemos decir que son áreas de extensión infinita.

Una nueva recta s dividirá al plano en dos nuevos semiplanos, cuya intersección con los anteriores determinarán cuatro regiones de área infinita, pero iguales dos a dos.

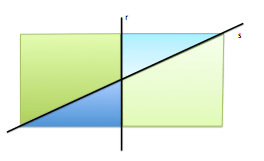
Existen tres sistemas de medida de los ángulos:

• Radianes : Valores comprendidos entre 0 y dos veces el valor de PI
• Sexagesimal: Valores comprendidos entre cero y 360
• Centesimal: Valores comprendidos entre cero y 400

Ángulo entre dos rectas

El concepto de ángulo se usa para medir o caracterizar un área infinita, una porción del plano que a su vez es la intersección de dos semiplanos.

Un ángulo es la parte del plano comprendida entre dos semirrectas que tienen el mismo punto de origen o vértice. Suelen medirse en unidades tales como el radián, el grado sexagesimal o el grado centesimal. (W)

Las primeras definiciones que se diero de estos conceptos se denominan definiciones clásicas:

Euclides define un ángulo como la inclinación mutua de dos líneas que se encuentran una a otra en un plano y no están en línea recta. Según Proclo, un ángulo debe ser una calidad o una cantidad, o una relación. El primer concepto fue utilizado por Eudemo de Rodas, que describió un ángulo como desviación de una línea recta; el segundo por Carpo de Antioquía, que lo vio como el intervalo o el espacio entre las líneas que se intersecaban; Euclides adoptó un tercer concepto, aunque sus definiciones de ángulos rectos, agudos, y obtusos son cuantitativas. (W)

El valor del ángulo entre dos rectas siempre se da como el menor de los dos que determinan.

Ángulo entre recta y circunferencia

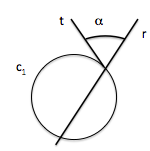
Para definir el ángulo que forman una recta y una circunferencia incidentes, determinaremos la tangente en el punto de intersección.

Reduciremos el problema al de dos rectas.

El ángulo que forman una recta y una circunferencia que se cortan, es el que forma la recta con la tangente a la circunferencia en uno de los puntos de intersección.

La recta puede cortar en dos puntos a la circunferencia; si realizamos el cálculo del ángulo en cualquiera de los puntos de intersección, el valor es el mismo.

Ángulo entre dos circunferencias

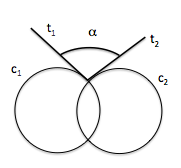
Para definir el ángulo que forman dos circunferencia incidentes, determinaremos las tangentes en uno de los puntos de intersección.

Reduciremos el problema al de dos rectas.

El ángulo que forman dos circunferencias que se cortan, es el que forman sus tangentes en cualquiera de sus puntos de intersección.

Las circunferencias pueden cortarse en dos puntos; si realizamos el cálculo del ángulo en cualquiera de los puntos de intersección, el valor es el mismo.