Inicio » Sin categoría
Archivos de la categoría: Sin categoría
Teorema de Thales
Uno de los teoremas más importantes de la geometría métrica es el enunciado por Thales de Mileto. Junto con el teorema de Pitágoras establecen las bases fundamentales de la axiomática de las geometrías métrica y proyectiva.


Tales de Mileto (en griego Θαλῆς ὁ Μιλήσιος) (ca. 630 – 545 a. C ) fue el iniciador de la indagación racional sobre el universo. Se le considera el primer filósofo de la historia de la filosofía occidental, y fue el fundador de la escuela jónica de filosofía, según el testimonio de Aristóteles. Fue el primero y más famoso de los Siete Sabios de Grecia (el sabio astrónomo), y habría tenido, según una tradición antigua no muy segura, como discípulo y protegido a Pitágoras.
Fue además uno de los más grandes matemáticos de su época, centrándose sus principales aportaciones en los fundamentos de la geometría.(W)
Enunciado del primer Teorema de Thales
El teorema de Thales establece la noción de semejanza entre dos triángulos relacionando la longitud de dos de sus lados. Permite definir un invariante proyectivo de aplicación a los sistemas de proyección cilíndricos: La razón simple.
Si cortamos dos rectas cualesquiera por varias rectas paralelas,los segmentos correspondientes en ambas son proporcionales,es decir, se corresponden en la igualdad ,en la suma y en la resta.

Si por un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes.(W)
El teorema establece las siguientes igualdades entre los cocientes de dos lados homólogos en dos triángulos semejantes:
- m/n = m’/n’
- m/n = (m+m’)/(n+n’)
- n/p = (n+n’)/p’
La semejanza entre dos triángulos nos permite por lo tanto establecer relaciones entre dos de sus lados determinando aspectos inherentes a la “forma” de dicho elemento geométrico, independientes de su “tamaño”. ¿Qué relaciones puedes observar en la siguiente figura?
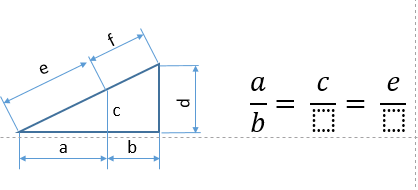
En la figura se observan dos triángulos semejantes, pero podemos encontrar nuevos triángulos semejantes a los anteriores mediante rectas paralelas a sus lados:
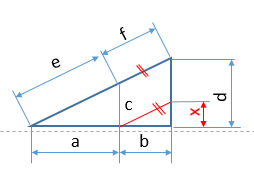
Aplicando las relaciones anteriores, por semejanza entre los triángulos más pequeños se tiene que:
a/c = b/x
pero como x= d – c
a/c = b/(d-c)
y reordenando obtenemos la solución al ejercicio propuesto
a/b=c/(d-c)
Aplicaciones: Escalas
El concepto de semejanza se asocia con el de escala. Dos formas semejantes (igual forma pero diferente tamaño) sólo varían en la escala de su representación.
La escala es la relación matemática que existe entre las dimensiones reales y las del dibujo que representa la realidad sobre un plano o un mapa.(W)
Escala = Medida lineal en el Dibujo/Medida lineal del objeto real
E= D / R
Por ejemplo, la escala E = 3/4 indica que de 4 unidades de medida del objeto real, tomamos 3 en el dibujo.
Elementos que forman una escala gráfica.
Una escala se construye sobre un soporte rectilíneo. Cada parte numerada se denomina módulo. La parte que se encuentra a la izquierda del cero se llama contraescala.

Construcción de Escalas
Como ejemplo de aplicación supongamos que queremos construir la escala 7/9.
Usaremos un soporte rectilíneo de longitud 7 unidades que representará las medidas del dibujo y una recta auxiliar de longitud nueve unidades unida por un extremo a la anterior que representará la medida de la realidad.
Uniremos los dos extremos libres de ambas rectas e iremos trazando paralelas a esta última recta por cada una de las unidades de la recta auxiliar.

Ejercícios
Los siguientes ejercicios permiten profundizar y asentar los conceptos tratados que serán fundamentales para, posteriormente, entender los invariantes proyectivos que usaremos en los sistemas de representación.
1.- División de un segmento s = AB en partes proporcionales a otros a, b, c.

2.- Si a/b= c/x, hallar el segmento x ,cuarta proporcional de tres segmentos a, b, c dados.
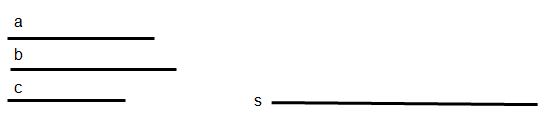
3.- Si a/b = b/x. Hallar el segmento x ,tercera proporcional de dos segmentos a, b dados.

4.- Hallar dos segmentos x é y, conocidas su suma s y su diferencia d.

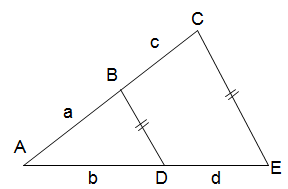
5-. En la figura adjunta se pueden establecer diferentes relaciones entre los segmentos obtenidos al seccionar dos rectas paralelas por otras dos rectas:
Indicar si la relación es verdadera (V) o falsa (F) en cada caso
- V F AD . AE = AB . BC
- V F AD / BC = AB / DE
- V F AB . DE = AD . BC
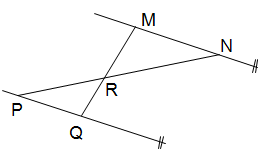
6.- En la figura adjunta se pueden establecer diferentes relaciones entre los segmentos obtenidos al seccionar dos rectas paralelas por otras dos rectas cualesquiera:
Indicar si la relación es verdadera (V) o falsa (F) en cada caso
- V F MN / NR = QP . QR
- V F MN . QR = MR . QP
- V F PR / RN = QR / RM
7.- Dado un segmento m, determinar dos segmentos p y q sabiendo que:
- m = q + p
- p/q =2/3
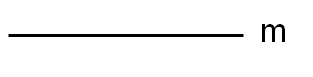
8.- Dado un segmento m, determinar dos segmentos p y q sabiendo que:
- m = q – p
- p/q =2/3
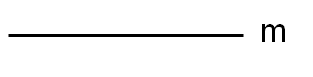

Comentarios recientes