Aplicación del teorema de Pitágoras: Ecuación de la circunferencia
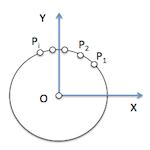
Una de las primeras aplicaciones que podemos encontrar en el teorema de Pitágoras, es su uso en la determinación de la ecuación de una circunferencia.
La relación métrica entre los dos catetos de un triángulo rectángulo son esencialmente la expresión del concepto de medida euclídeo.
Los puntos de una circunferencia se encuentran a igual distancia de un punto, O, denominado centro de la circunferencia.
Una circunferencia es el lugar geométrico de los puntos de un plano que equidistan de otro punto fijo y coplanario llamado centro, en una cantidad constante llamada radio.(W)
Para determinar la ecuación de la circunferencia analizaremos primero el caso en que ésta se encuentre con su centro en el origen del sistema de referencia. Posteriormente podremos generalizar dicha ecuación para que dicho centro se encuentre en cualquier posición del plano.

La distancia de cualquier punto P(x,y) de la circunferencia a su centro O es igual a su radio R.
En la figura se aprecia que esta distanca, R, es la hipotenusa de un triángulo rectángulo que tiene por catetos, C1 y C2, a las coordenadas x e y del punto P. Por ello, aplicando el teorema de pitágoras:

Podemos mover la circunferencia, desplazando el centro de dicha circunferencia a cualquier punto del plano. Las coordenadas de su centro O serán (Xo, Yo), como se aprecia en la figura:
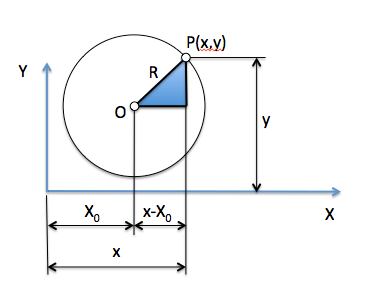
Los puntos de la circunferencia seguiran a distancia R del centro, pero en este caso los catetos del triángulo, en el sistema de referencia XY ya no serán las coordenadas (x,y) del punto P, sino la diferencia entre estas y las del centro (Xo,Yo).
Los catetos del triángulo anterior valdrán:
- C1=x-Xo
- C2=y-Yo
Por lo tanto, aplicando de nuevo el teorema de Pitágoras, la nueva ecuación de la circunferencia será:

Podemos desarrollar esta ecuación y agrupar los coeficientes y las variables de forma ordenada, con lo que tendremos:

Simplificando y agrupando términos:

En los que los coeficientes A, B y C valen:

¿Sabrías determinar la ecuación de la circunferencia de centro el punto O(3,4) que pase por el origen de coordenadas (0,0) ?
Teorema de Pitágoras

La geometría métrica se fundamenta en el conocido teorema de Pitágoras, que establece la relación métrica entre los lados de un triángulo rectángulo.
El concepto de medida del espacio euclídeo lo adopta en su definición de distancia, y las relaciones geométricas derivadas son de suma importancia.
A pitágoras debemos otros teoremas menos conocidos, así como el reconocimiento a la escuela de geómetras que creó, de la que hoy nos beneficiamos todos.
Pitágoras de Samos (aproximadamente 582 – 507 a. C., en griego: Πυθαγόρας ο Σάμιος) fue un filósofo y matemático griego, famoso sobre todo por el Teorema de Pitágoras, que en realidad pertenece a la escuela pitagórica y no solo a Pitágoras. Su escuela afirmaba «todo es número», por ello, se dedicó al estudió y clasificación de los números.(W)
Enunciado del Teorema de Pitágoras
El teorema de Pitágoras se puede enunciar de diferentes formas. Una de las más utilizadas es:
En todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.(w)
Existen diferentes demostraciones de este importante teorema que es la base de la geometría métrica.
El Chou Pei es una obra matemática de datación discutida en algunos lugares, aunque se acepta mayoritariamente que fue escrita entre el 500 y el 300 a. C.Se cree que Pitágoras no conoció esta obra. En cuanto al Chui Chang parece que es posterior, está fechado en torno al año 250 a. C.
El Chou Pei demuestra el teorema construyendo un cuadrado de lado (a+b) que se parte en cuatro triángulos de base a y altura b, y un cuadrado de lado c (W)
Matemáticamente se puede enunciar con la siguiente ecuación:

Esta ecuación expresa que el área de un cuadrado de lado “a” es igual a la suma de las áreas de dos cuadrados, uno de lado “b” y otro de lado “c”. Si denominamos “a” a la hipotenusa (lado más largo) de un triángulo rectángulo y “b” y “c” a los catetos, gráficamente se puede representar con la siguiente figura.

Para demostrar que esta ecuación se cumple, usaremos dos nuevas figuras obtenidas a partir de cuadrados de lado “b+c”. En el primero se dibuja un cuadrado inscrito de lado a cuyo área será el cuadrado de este lado. Para completar el área del cuadrado del que hemos partido deberemos añadir cuatro triángulos rectángulos iguales (azul claro).
En la figura de la derecha se han formado dos cuadrados, uno de lado “b” y otro de lado “c”. Para completar el área total se necesitan de nuevo cuatro triángulos rectángulos, lo mismo que en el caso anterior, lo que permite asegurar que el cuadrado de lado “a” tiene un área igual a la de la suma de los otros dos cuadrados.

Esta demostración tiene el encanto de ser muy gráfica y sencilla, sin apenas operaciones matemáticas.
Propiedades del triangulo rectángulo
Hay dos propiedades del triángulo rectángulo (un ángulo es recto) que tienen especial importancia para el desarrollo de conceptos más elaborados como son los de potencia e inversión que permiten desarrollar los modelos que analizan las tangencias Son los denominados teoremas de la altura y del cateto.
En la figura se ha representado un triángulo rectángulo que reposa sobre su hipotenusa. La altura del triángulo es la distancia del vértice “A” a la hipotenusa (su base).

Teoremas del cateto y de la altura.
Ambos teoremas se basan en el conocido teorema de Thales, que establece una relación entre los lados de dos triángulos semejantes.
Si dos triángulos tienen dos ángulos iguales, el tercero también lo es. Esto es así ya que la suma de los ángulos internos de un triángulo siempre son 180º sexagesimales.
Para demostrar que dos triángulos son semejantes basta con demostrar que tienen dos ángulos iguales.
En la figura anterior podemos encontrar tres triángulos semejantes: ABC, ABH y HCA. Los tres triángulos tienen un ángulo recto, y dos a dos comparten un ángulo, luego el tercero vale lo mismo.
Podemos por tanto, aplicando Thales, establecer algunas igualdades como:
BA/BC = BH/BA o AH/HC = BH/AH
siendo BA la distancia entre los puntos A y B etc.
Los siguientes teoremas se obtienen directamente de las relaciones anteriores:
•Teorema del cateto-.El cateto de un triángulo rectángulo es media proporcional entre la hipotenusa y la proyección de dicho cateto sobre la hipotenusa.
- BA es el valor de uno de los catetos,
- BC el de la hipotenusa
- BH es la proyección de BA sobre la hipotenusa
•Teorema de la altura-.La altura de un triángulo rectángulo medida sobre su hipotenusa es media proporcional entre los dos segmentos en que la divide.
- AH es la altura del triángulo medido sobre la hipotenusa
- BH y HC los dos segmentos en que divide la altura a la hipotenusa
Ejemplo de aplicación teorema del cateto
Datos (a, b, x. x = a. b ).
Incógnita ( Hallar el segmento x media proporcional, entre dos segmentos a , b dados)

Ejemplo de aplicación teorema de la altura
Datos (a, b, x. x = a. b ).
Incógnita ( Hallar el segmento x media proporcional, entre dos segmentos a , b dados)

Datos (m, s, x + y = s , x .y = m. m).
Incógnita (Hallar dos segmentos x e y conocida su suma s y su media proporcional m o su producto m. m.)
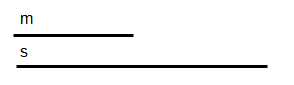
Ejemplo de aplicación del triángulo rectángulo
Dados dos puntos A y B. Trazar por ellos dos rectas paralelas que disten la magnitud m dada.

Test de autoevaluación
Se deberá marcar V (verdadero) o F (Falso) cada una de las relaciones siguientes
Test 1
  |
Utilizaremos diferentes subíndices para identificar a los elementos.
Por ejemplo, un triángulo tiene tres alturas. Si la medimos desde el vértice “A” la etiquetaremos con el subíndice “a” en minúscula.
Los lados opuestos a un vértice se etiquetarán con la misma letra pero en minúsculas
 | Utilizaremos diferentes subíndices para identificar a los elementos. Por ejemplo, un triángulo tiene tres alturas. Si la medimos desde el vértice “A” la etiquetaremos con el subíndice “a” en minúscula. Los lados opuestos a un vértice se etiquetarán con la misma letra pero en minúsculas |
 | Para contestar a las preguntas, se recomienda buscar primero las posibles relaciones que se derivan de aplicar los teoremas expuestos (cateto y altura). |
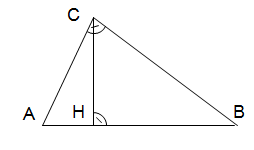 | El punto “H” se denomina pie de la altura hc H divide a la hipotenusa en dos segmentos. En este caso se ha utilizado incorrectamente la designación de los vértices del triángulo, ya que se debe usar la letra “A” para el que contiene el ángulo recto. |
Recuerda que debes identificar gráficamente los segmentos que se relacionan con la figura.
El interés es formar gráficamente de forma que las expresiones matemáticas no sean el nucleo formativo. Las construcciones gráficas son las que deben primar en un aprendizaje de la geometría básica para poder alcanzar altos niveles de abstracción.

Teorema de Thales
Uno de los teoremas más importantes de la geometría métrica es el enunciado por Thales de Mileto. Junto con el teorema de Pitágoras establecen las bases fundamentales de la axiomática de las geometrías métrica y proyectiva.


Tales de Mileto (en griego Θαλῆς ὁ Μιλήσιος) (ca. 630 – 545 a. C ) fue el iniciador de la indagación racional sobre el universo. Se le considera el primer filósofo de la historia de la filosofía occidental, y fue el fundador de la escuela jónica de filosofía, según el testimonio de Aristóteles. Fue el primero y más famoso de los Siete Sabios de Grecia (el sabio astrónomo), y habría tenido, según una tradición antigua no muy segura, como discípulo y protegido a Pitágoras.
Fue además uno de los más grandes matemáticos de su época, centrándose sus principales aportaciones en los fundamentos de la geometría.(W)
Enunciado del primer Teorema de Thales
El teorema de Thales establece la noción de semejanza entre dos triángulos relacionando la longitud de dos de sus lados. Permite definir un invariante proyectivo de aplicación a los sistemas de proyección cilíndricos: La razón simple.
Si cortamos dos rectas cualesquiera por varias rectas paralelas,los segmentos correspondientes en ambas son proporcionales,es decir, se corresponden en la igualdad ,en la suma y en la resta.

Si por un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes.(W)
El teorema establece las siguientes igualdades entre los cocientes de dos lados homólogos en dos triángulos semejantes:
- m/n = m’/n’
- m/n = (m+m’)/(n+n’)
- n/p = (n+n’)/p’
La semejanza entre dos triángulos nos permite por lo tanto establecer relaciones entre dos de sus lados determinando aspectos inherentes a la “forma” de dicho elemento geométrico, independientes de su “tamaño”. ¿Qué relaciones puedes observar en la siguiente figura?
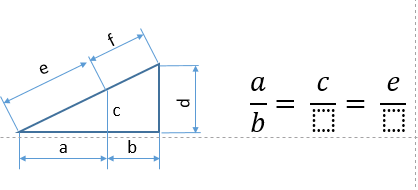
En la figura se observan dos triángulos semejantes, pero podemos encontrar nuevos triángulos semejantes a los anteriores mediante rectas paralelas a sus lados:
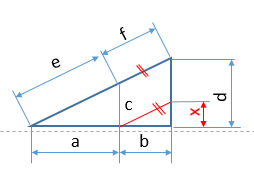
Aplicando las relaciones anteriores, por semejanza entre los triángulos más pequeños se tiene que:
a/c = b/x
pero como x= d – c
a/c = b/(d-c)
y reordenando obtenemos la solución al ejercicio propuesto
a/b=c/(d-c)
Aplicaciones: Escalas
El concepto de semejanza se asocia con el de escala. Dos formas semejantes (igual forma pero diferente tamaño) sólo varían en la escala de su representación.
La escala es la relación matemática que existe entre las dimensiones reales y las del dibujo que representa la realidad sobre un plano o un mapa.(W)
Escala = Medida lineal en el Dibujo/Medida lineal del objeto real
E= D / R
Por ejemplo, la escala E = 3/4 indica que de 4 unidades de medida del objeto real, tomamos 3 en el dibujo.
Elementos que forman una escala gráfica.
Una escala se construye sobre un soporte rectilíneo. Cada parte numerada se denomina módulo. La parte que se encuentra a la izquierda del cero se llama contraescala.

Construcción de Escalas
Como ejemplo de aplicación supongamos que queremos construir la escala 7/9.
Usaremos un soporte rectilíneo de longitud 7 unidades que representará las medidas del dibujo y una recta auxiliar de longitud nueve unidades unida por un extremo a la anterior que representará la medida de la realidad.
Uniremos los dos extremos libres de ambas rectas e iremos trazando paralelas a esta última recta por cada una de las unidades de la recta auxiliar.

Ejercícios
Los siguientes ejercicios permiten profundizar y asentar los conceptos tratados que serán fundamentales para, posteriormente, entender los invariantes proyectivos que usaremos en los sistemas de representación.
1.- División de un segmento s = AB en partes proporcionales a otros a, b, c.

2.- Si a/b= c/x, hallar el segmento x ,cuarta proporcional de tres segmentos a, b, c dados.
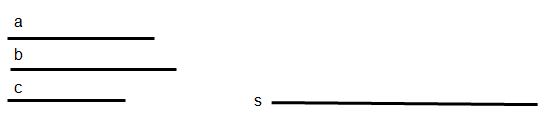
3.- Si a/b = b/x. Hallar el segmento x ,tercera proporcional de dos segmentos a, b dados.

4.- Hallar dos segmentos x é y, conocidas su suma s y su diferencia d.

5-. En la figura adjunta se pueden establecer diferentes relaciones entre los segmentos obtenidos al seccionar dos rectas paralelas por otras dos rectas:
Indicar si la relación es verdadera (V) o falsa (F) en cada caso
- V F AD . AE = AB . BC
- V F AD / BC = AB / DE
- V F AB . DE = AD . BC
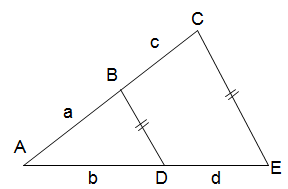
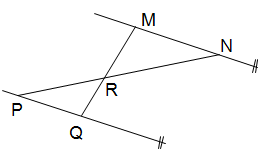
6.- En la figura adjunta se pueden establecer diferentes relaciones entre los segmentos obtenidos al seccionar dos rectas paralelas por otras dos rectas cualesquiera:
Indicar si la relación es verdadera (V) o falsa (F) en cada caso
- V F MN / NR = QP . QR
- V F MN . QR = MR . QP
- V F PR / RN = QR / RM
7.- Dado un segmento m, determinar dos segmentos p y q sabiendo que:
- m = q + p
- p/q =2/3
8.- Dado un segmento m, determinar dos segmentos p y q sabiendo que:
- m = q – p
- p/q =2/3
Ángulos en la circunferencia : Central e inscrito
En geometría métrica hay dos conceptos de medida sobre los que se basa su modelo axiomático:
medidas lineales y medidas angulares.
La medida lineal se apoya en el teorema de Pitágoras, y la relación entre este tipo de medidas en el teorema de Thales.
La medida angular la expresamos a partir de relaciones sobre una circunferencia y junto a las anteriores permiten describir la magnitud de las figuras geométricas.
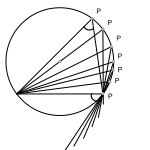
- Ángulo Central -. Es aquel que tiene su vértice en el centro en la circunferencia y tiene por medida el arco comprendido.
- Ángulo inscrito -. es aquel que tiene su vértice en la circunferencia y sus lados son cuerdas.
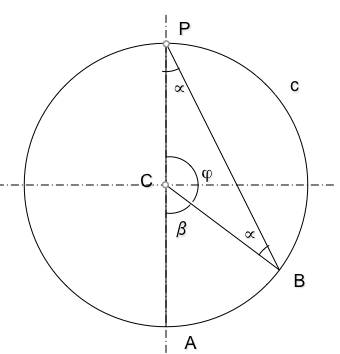
Un ángulo inscrito mide la mitad del ángulo central que abarca el mismo arco.
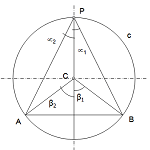
La suma de ángulos internos de un triángulo es igual a dos rectos, por lo que en el triángulo CBP, que es isósceles (dos ángulos iguales) se cumplirá la relación:
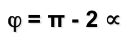
Por lo que tendremos que

Y como consecuencia deduciremos que el ángulo central es el doble que el inscrito
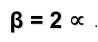
Es fácil generalizar este concepto para posiciones del punto P que no sean tan particulares, ya que podemos descomponer el ángulo en dos y aplicar el mismo razonamiento.
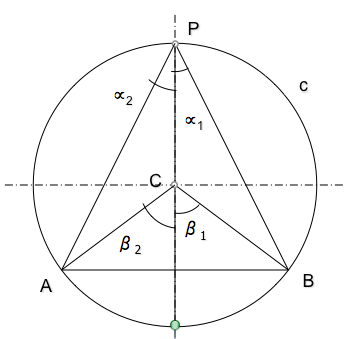
Por ejemplo, si desplazamos el punto P a lo largo de la circunferencia, el ángulo central será la suma de los dos ángulos centrales en que se puede descomponer, siendo por tanto indiferente la posición del punto P.
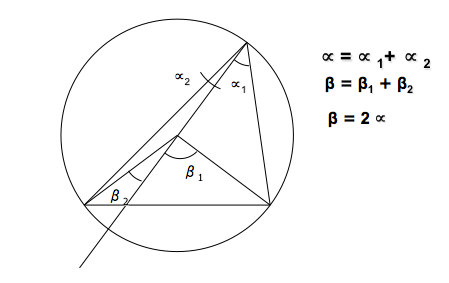
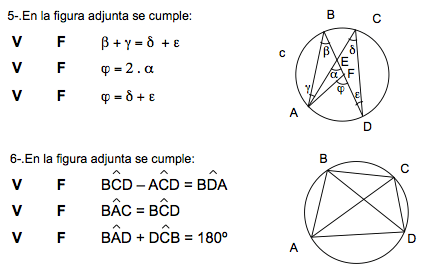
Ejercicios
Nociones sobre ángulos
Los elementos geométricos en el plano que se cortan, rectas y circunferencias, pueden caracterizar su intersección mediante un valor denominado ángulo.
La noción de ángulo entre dos rectas es la más elemental entre las que se dan entre rectas y circunferencias.
A partir de la definición elemental del ángulo entre dos rectas, podremos definir el ángulo formado entre una recta y una circunferencia o el que forman dos circunferencias coplanarias.
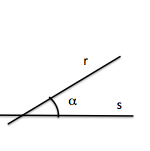
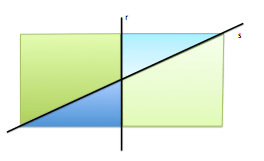
Para definir el concepto de ángulo, previamente, debemos recordar que una recta r divide a un plano en dos semiplanos.
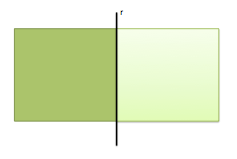
La recta r, tal y como se aprecia en la imagen anterior, divide al plano en dos semiplanos iguales. El área de cada uno de estos semiplanos no es medible. Podemos decir que son áreas de extensión infinita.
Una nueva recta s dividirá al plano en dos nuevos semiplanos, cuya intersección con los anteriores determinarán cuatro regiones de área infinita, pero iguales dos a dos.
Existen tres sistemas de medida de los ángulos:
- Radianes : Valores comprendidos entre 0 y dos veces el valor de PI
- Sexagesimal: Valores comprendidos entre cero y 360
- Centesimal: Valores comprendidos entre cero y 400
Ángulo entre dos rectas
El concepto de ángulo se usa para medir o caracterizar un área infinita, una porción del plano que a su vez es la intersección de dos semiplanos.
Un ángulo es la parte del plano comprendida entre dos semirrectas que tienen el mismo punto de origen o vértice. Suelen medirse en unidades tales como el radián, el grado sexagesimal o el grado centesimal. (W)
Las primeras definiciones que se diero de estos conceptos se denominan definiciones clásicas:
Euclides define un ángulo como la inclinación mutua de dos líneas que se encuentran una a otra en un plano y no están en línea recta. Según Proclo, un ángulo debe ser una calidad o una cantidad, o una relación. El primer concepto fue utilizado por Eudemo de Rodas, que describió un ángulo como desviación de una línea recta; el segundo por Carpo de Antioquía, que lo vio como el intervalo o el espacio entre las líneas que se intersecaban; Euclides adoptó un tercer concepto, aunque sus definiciones de ángulos rectos, agudos, y obtusos son cuantitativas. (W)
El valor del ángulo entre dos rectas siempre se da como el menor de los dos que determinan.
Ángulo entre recta y circunferencia
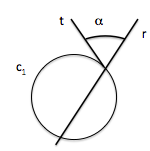
Para definir el ángulo que forman una recta y una circunferencia incidentes, determinaremos la tangente en el punto de intersección.
Reduciremos el problema al de dos rectas.
El ángulo que forman una recta y una circunferencia que se cortan, es el que forma la recta con la tangente a la circunferencia en uno de los puntos de intersección.
La recta puede cortar en dos puntos a la circunferencia; si realizamos el cálculo del ángulo en cualquiera de los puntos de intersección, el valor es el mismo.
Ángulo entre dos circunferencias
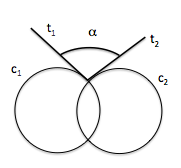
Para definir el ángulo que forman dos circunferencia incidentes, determinaremos las tangentes en uno de los puntos de intersección.
Reduciremos el problema al de dos rectas.
El ángulo que forman dos circunferencias que se cortan, es el que forman sus tangentes en cualquiera de sus puntos de intersección.
Las circunferencias pueden cortarse en dos puntos; si realizamos el cálculo del ángulo en cualquiera de los puntos de intersección, el valor es el mismo.
Secuencia de aprendizaje de la Geometría Métrica I
La geometría métrica que se aplica en el Espacio Euclídeo se basa en los teoremas de Thales y Pitágoras.
Las nociones sobre la relación entre los ángulos inscritos y central en una circunferencia completan los elementos básicos de aprendizaje para entender la Geometría Métrica.
Las unidades didácticas presentan de forma secuencial el conjunto de conceptos que fundamentan las construcciones geométricas. Añaden ejercicios básicos que refuerzan y asientan estos conceptos.
Al abordar el estudio de una ciencia podemos seguir diferentes trayectorias que conducen al aprendizaje. El encadenamiento de conceptos ligados unos a otros nos permitirá generar una representación mental de los modelos abstractos, facilitando su asimilación y posterior aplicación en la resolución de problemas.
La geometría no es muy diferente en este aspecto a otras disciplinas pero sin embargo, en niveles iniciales de su introducción en el bachillerato ha sido “descrita” como un conjunto de “trazados de carácter mecanicista” que permiten resolver los problemas sin una adecuada justificación. Lejos de esta interpretación, algunos tratados de geometría establecen itinerarios formativos que simplifican el aprendizaje de esta ciencia.
La geometría (del latín geometrĭa, que proviene del idioma griego γεωμετρία, geo tierra ymetria medida), es una rama de la matemática que se ocupa del estudio de las propiedades de las figuras geométricas en el plano o el espacio, como son: puntos, rectas, planos, politopos (incluyendo paralelas, perpendiculares, curvas, superficies, polígonos,poliedros, etc.).(W)
En estas páginas se proponen dos imágenes que resumen una posible estrategia o secuencia de incorporación progresiva de los conceptos básicos de esta rama de la ciencia en la formación de nuestros alumnos.
En un primer nivel formativo se establecerían los conceptos básicos sobre los que se apoyarán los desarrollos posteriores:
- Teorema de Thales
- Teorema de Pitágoras
- Arco capaz
- Concepto de Potencia
- Problema Fundamental de Tangencias
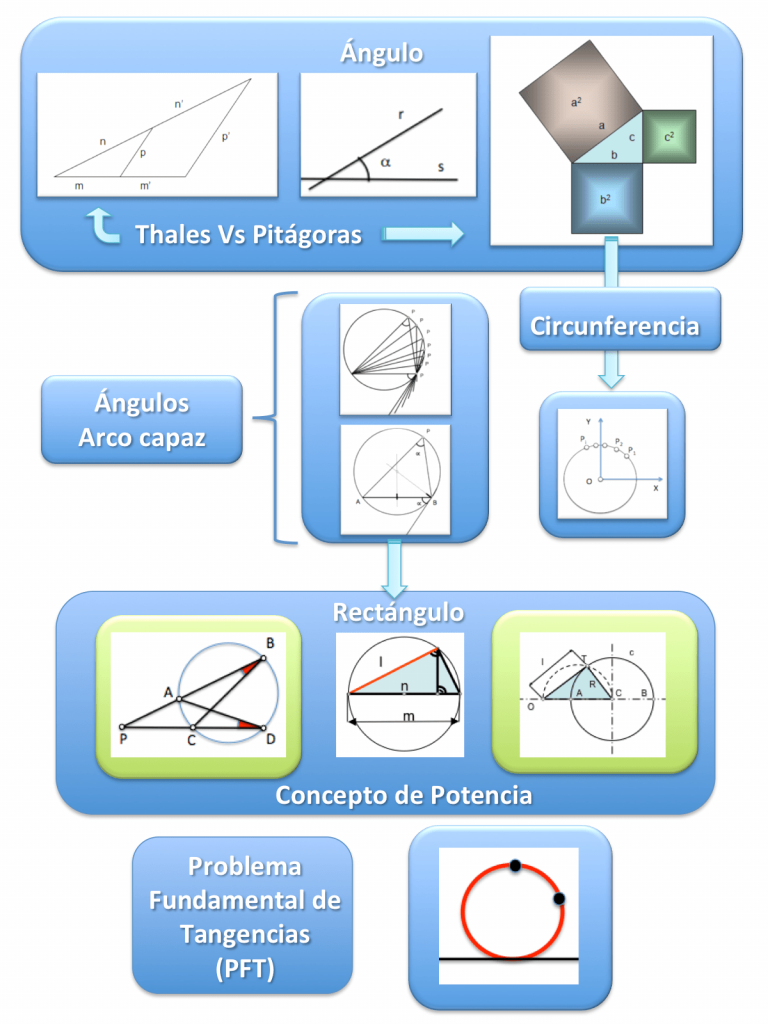
Tras la incorporación de los conceptos básicos anteriores podemos avanzar en el estudio vertical de detalle de los conceptos básicos aprendidos. Así, el concepto elemental de “potencia” nos permitirá acometer el “problema fundamental de tangencias” en cualquiera de sus variantes, y la incorporación del concepto de “Haces de circunferencias” facilitará una generalización más amplia del mismo.
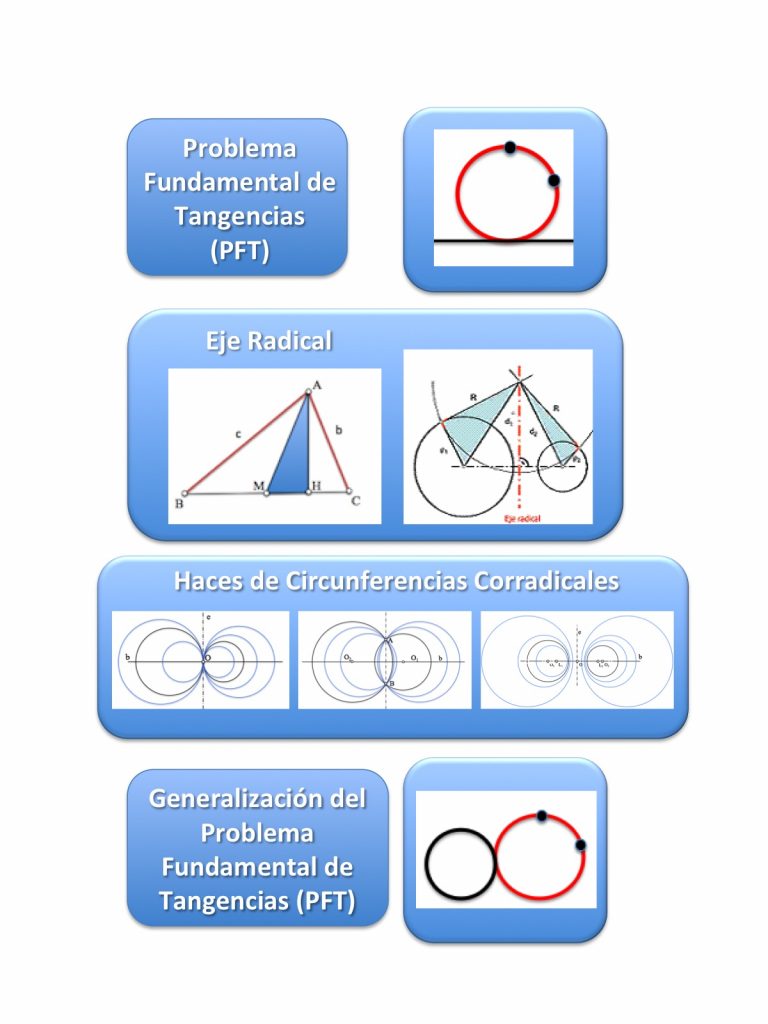
Esta secuencia puede completarse posteriormente con el estudio clásico de los problemas de tangencias y el estudio métrico de las cónicas.

Comentarios recientes