Nociones sobre ángulos
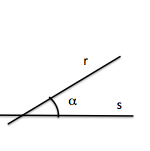
Los elementos geométricos en el plano que se cortan, rectas y circunferencias, pueden caracterizar su intersección mediante un valor denominado ángulo.
La noción de ángulo entre dos rectas es la más elemental entre las que se dan entre rectas y circunferencias.
A partir de la definición elemental del ángulo entre dos rectas, podremos definir el ángulo formado entre una recta y una circunferencia o el que forman dos circunferencias coplanarias.
Para definir el concepto de ángulo, previamente, debemos recordar que una recta r divide a un plano en dos semiplanos.
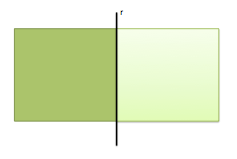
La recta r, tal y como se aprecia en la imagen anterior, divide al plano en dos semiplanos iguales. El área de cada uno de estos semiplanos no es medible. Podemos decir que son áreas de extensión infinita.
Una nueva recta s dividirá al plano en dos nuevos semiplanos, cuya intersección con los anteriores determinarán cuatro regiones de área infinita, pero iguales dos a dos.
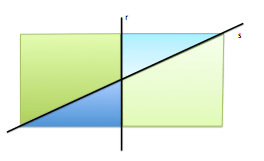
Existen tres sistemas de medida de los ángulos:
- Radianes : Valores comprendidos entre 0 y dos veces el valor de PI
- Sexagesimal: Valores comprendidos entre cero y 360
- Centesimal: Valores comprendidos entre cero y 400
Ángulo entre dos rectas
El concepto de ángulo se usa para medir o caracterizar un área infinita, una porción del plano que a su vez es la intersección de dos semiplanos.
Un ángulo es la parte del plano comprendida entre dos semirrectas que tienen el mismo punto de origen o vértice. Suelen medirse en unidades tales como el radián, el grado sexagesimal o el grado centesimal. (W)
Las primeras definiciones que se diero de estos conceptos se denominan definiciones clásicas:
Euclides define un ángulo como la inclinación mutua de dos líneas que se encuentran una a otra en un plano y no están en línea recta. Según Proclo, un ángulo debe ser una calidad o una cantidad, o una relación. El primer concepto fue utilizado por Eudemo de Rodas, que describió un ángulo como desviación de una línea recta; el segundo por Carpo de Antioquía, que lo vio como el intervalo o el espacio entre las líneas que se intersecaban; Euclides adoptó un tercer concepto, aunque sus definiciones de ángulos rectos, agudos, y obtusos son cuantitativas. (W)
El valor del ángulo entre dos rectas siempre se da como el menor de los dos que determinan.
Ángulo entre recta y circunferencia
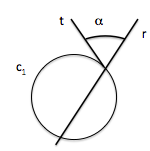
Para definir el ángulo que forman una recta y una circunferencia incidentes, determinaremos la tangente en el punto de intersección.
Reduciremos el problema al de dos rectas.
El ángulo que forman una recta y una circunferencia que se cortan, es el que forma la recta con la tangente a la circunferencia en uno de los puntos de intersección.
La recta puede cortar en dos puntos a la circunferencia; si realizamos el cálculo del ángulo en cualquiera de los puntos de intersección, el valor es el mismo.
Ángulo entre dos circunferencias
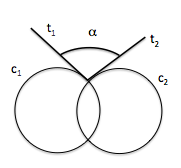
Para definir el ángulo que forman dos circunferencia incidentes, determinaremos las tangentes en uno de los puntos de intersección.
Reduciremos el problema al de dos rectas.
El ángulo que forman dos circunferencias que se cortan, es el que forman sus tangentes en cualquiera de sus puntos de intersección.
Las circunferencias pueden cortarse en dos puntos; si realizamos el cálculo del ángulo en cualquiera de los puntos de intersección, el valor es el mismo.
Secuencia de aprendizaje de la Geometría Métrica I
La geometría métrica que se aplica en el Espacio Euclídeo se basa en los teoremas de Thales y Pitágoras.
Las nociones sobre la relación entre los ángulos inscritos y central en una circunferencia completan los elementos básicos de aprendizaje para entender la Geometría Métrica.
Las unidades didácticas presentan de forma secuencial el conjunto de conceptos que fundamentan las construcciones geométricas. Añaden ejercicios básicos que refuerzan y asientan estos conceptos.
Al abordar el estudio de una ciencia podemos seguir diferentes trayectorias que conducen al aprendizaje. El encadenamiento de conceptos ligados unos a otros nos permitirá generar una representación mental de los modelos abstractos, facilitando su asimilación y posterior aplicación en la resolución de problemas.
La geometría no es muy diferente en este aspecto a otras disciplinas pero sin embargo, en niveles iniciales de su introducción en el bachillerato ha sido “descrita” como un conjunto de “trazados de carácter mecanicista” que permiten resolver los problemas sin una adecuada justificación. Lejos de esta interpretación, algunos tratados de geometría establecen itinerarios formativos que simplifican el aprendizaje de esta ciencia.
La geometría (del latín geometrĭa, que proviene del idioma griego γεωμετρία, geo tierra ymetria medida), es una rama de la matemática que se ocupa del estudio de las propiedades de las figuras geométricas en el plano o el espacio, como son: puntos, rectas, planos, politopos (incluyendo paralelas, perpendiculares, curvas, superficies, polígonos,poliedros, etc.).(W)
En estas páginas se proponen dos imágenes que resumen una posible estrategia o secuencia de incorporación progresiva de los conceptos básicos de esta rama de la ciencia en la formación de nuestros alumnos.
En un primer nivel formativo se establecerían los conceptos básicos sobre los que se apoyarán los desarrollos posteriores:
- Teorema de Thales
- Teorema de Pitágoras
- Arco capaz
- Concepto de Potencia
- Problema Fundamental de Tangencias
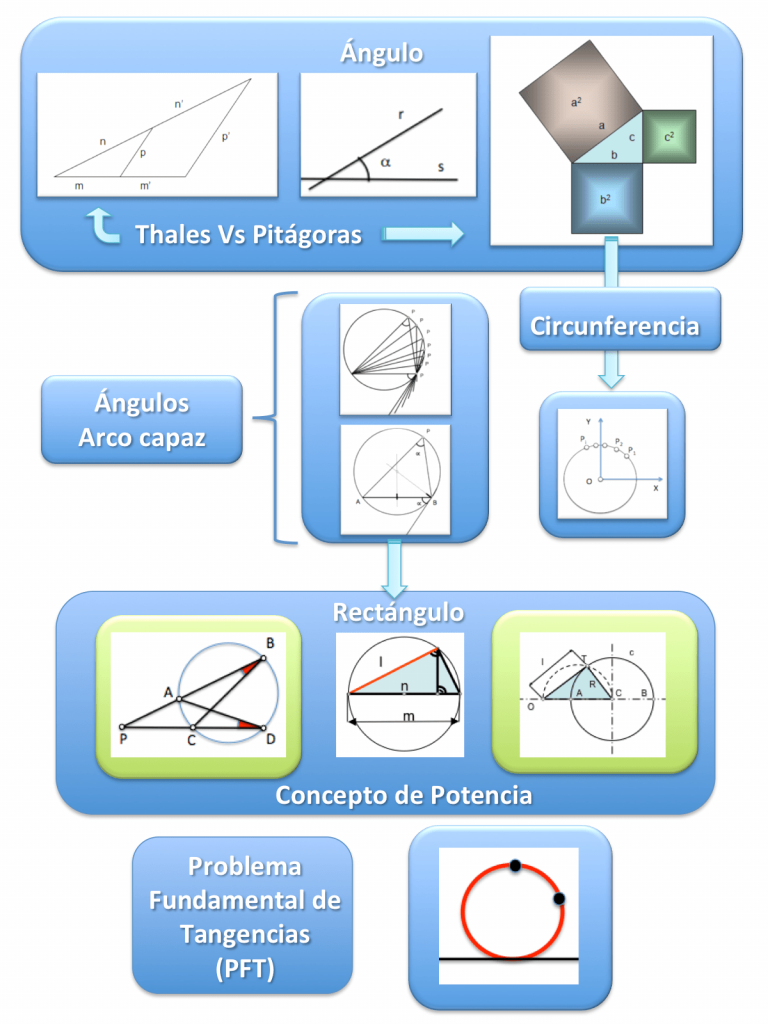
Tras la incorporación de los conceptos básicos anteriores podemos avanzar en el estudio vertical de detalle de los conceptos básicos aprendidos. Así, el concepto elemental de “potencia” nos permitirá acometer el “problema fundamental de tangencias” en cualquiera de sus variantes, y la incorporación del concepto de “Haces de circunferencias” facilitará una generalización más amplia del mismo.
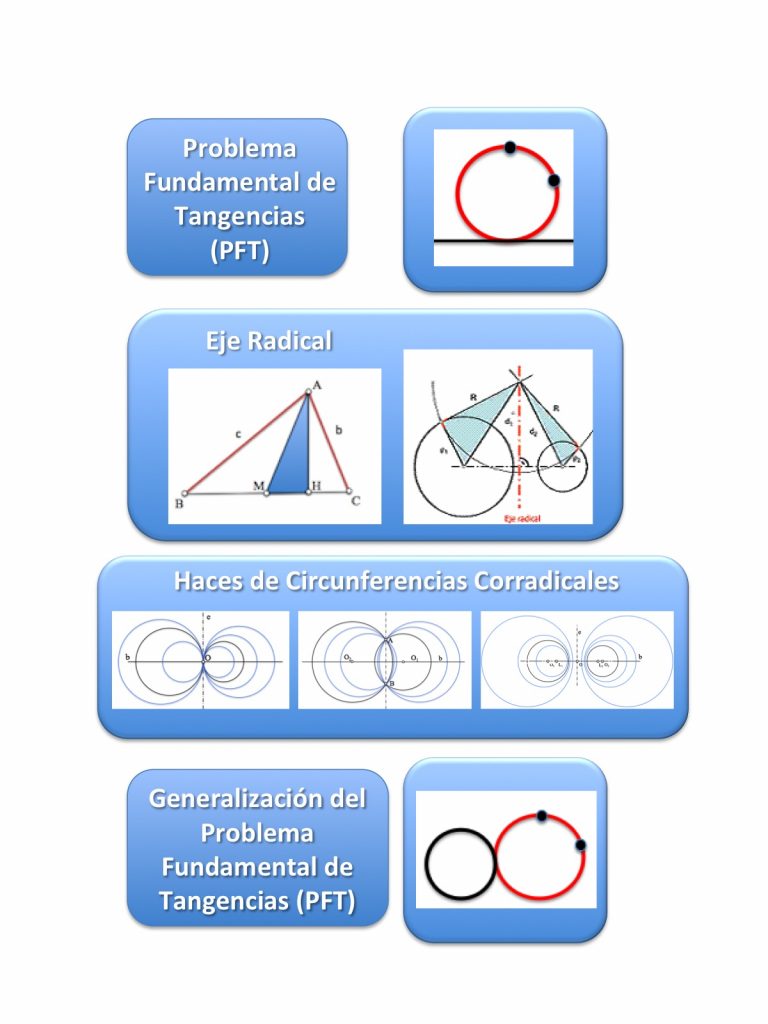
Esta secuencia puede completarse posteriormente con el estudio clásico de los problemas de tangencias y el estudio métrico de las cónicas.

Comentarios recientes