Una de las primeras aplicaciones que podemos encontrar en el teorema de Pitágoras, es su uso en la determinación de la ecuación de una circunferencia.

La relación métrica entre los dos catetos de un triángulo rectángulo son esencialmente la expresión del concepto de medida euclídeo.

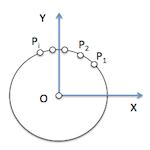
Los puntos de una circunferencia se encuentran a igual distancia de un punto, O, denominado centro de la circunferencia.

Una circunferencia es el lugar geométrico de los puntos de un plano que equidistan de otro punto fijo y coplanario llamado centro, en una cantidad constante llamada radio.(W)

Para determinar la ecuación de la circunferencia analizaremos primero el caso en que ésta se encuentre con su centro en el origen del sistema de referencia. Posteriormente podremos generalizar dicha ecuación para que dicho centro se encuentre en cualquier posición del plano.

La distancia de cualquier punto P(x,y) de la circunferencia a su centro O es igual a su radio R.

En la figura se aprecia que esta distanca, R, es la hipotenusa de un triángulo rectángulo que tiene por catetos, C₁ y C₂, a las coordenadas x e y del punto P. Por ello, aplicando el teorema de pitágoras:

Podemos mover la circunferencia, desplazando el centro de dicha circunferencia a cualquier punto del plano. Las coordenadas de su centro O serán (Xo, Yo), como se aprecia en la figura:

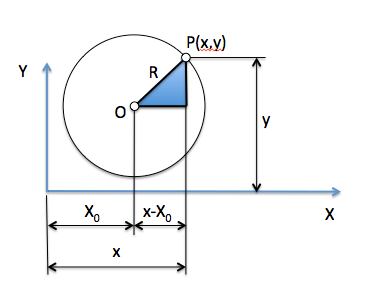
Los puntos de la circunferencia seguiran a distancia R del centro, pero en este caso los catetos del triángulo, en el sistema de referencia XY ya no serán las coordenadas (x,y) del punto P, sino la diferencia entre estas y las del centro (Xo,Yo).

Los catetos del triángulo anterior valdrán:

• C₁=x-Xo
• C₂=y-Yo

Por lo tanto, aplicando de nuevo el teorema de Pitágoras, la nueva ecuación de la circunferencia será:

Podemos desarrollar esta ecuación y agrupar los coeficientes y las variables de forma ordenada, con lo que tendremos:

Simplificando y agrupando términos:

En los que los coeficientes A, B y C valen:

¿Sabrías determinar la ecuación de la circunferencia de centro el punto O(3,4) que pase por el origen de coordenadas (0,0) ?

Aplicación del teorema de Pitágoras: Ecuación de la circunferencia por jjaliaga está licenciado bajo una Licencia Creative Commons Atribución-NoComercial 4.0 Internacional.