Redes complejas en el estudio de resonancias magnéticas funcionales.
Propuesta de TFG para alumnos de GIB o de GITST
Codirectores:
Salvador Jiménez Burillo, s.jimenez@upm.es
ETSI Telecomunicación, UPM. Dpto. Matemática Aplicada a las TIC
Jesús Tornero López, jesus.tornero@lmh.es
Hospital Los Madroños
Descripción:
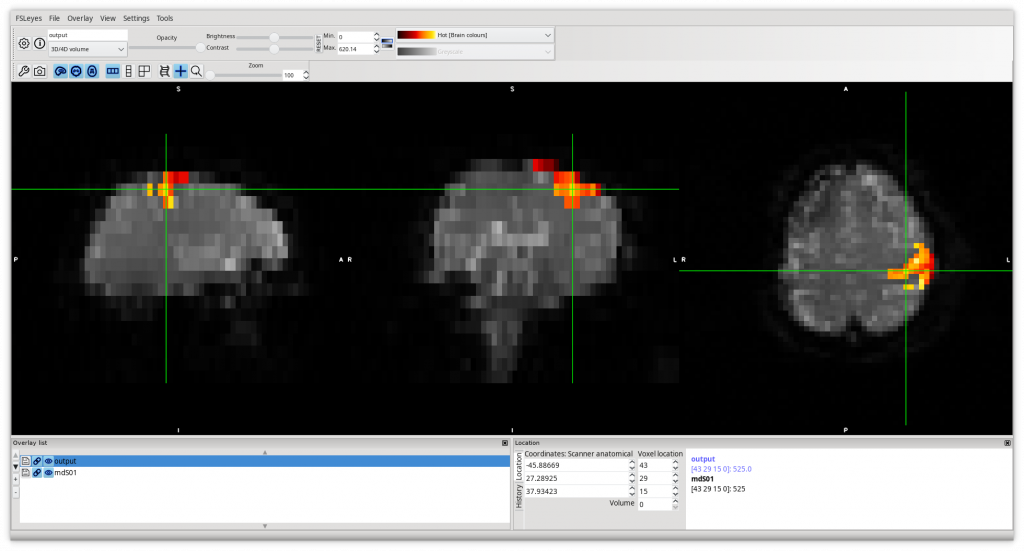
el TFT tiene por objetivo el estudio de redes complejas asociadas a resonancias magnéticas funcionales y su posterior análisis.
Las pruebas corresponden a un estudio con sujetos sanos o pacientes con alguna patología neurofuncional. El estudio consiste en la construcción de redes considerando diferentes filtrados, establecer sus características en función de ellos, e identificar regiones anatómicas con alta conectividad relacionadas con el paradigma funcional. El estudio se realiza mediante el software utilizado por el grupo investigador.
El trabajo se integra dentro de un entorno de investigación que sobre estos temas realizan los dos codirectores en contacto con la unidad de neurorehabilitación del hospital Los Madroños.
Electromagnetismo computacional
Valentín de la Rubia Hernández valentin.delarubia@upm.es A-313
Se oferta una serie de proyectos dentro de la línea de investigación de electromagnetismo computacional. Estos proyectos tienen como denominador común la resolución de la ecuaciones de Maxwell de forma eficiente mediante ordenador con el objetivo de realizar diseños de distintos dispositivos electromagnéticos que aparecen en todo sistema de telecomunicación, como por ejemplo filtros, diplexores, triplexores, antenas y array de antenas en las bandas de microondas y milimétricas.
⋆Desarrollo e implementación de métodos numéricos en electromagnetismo.
⋆Diseño de filtros y diplexores para 5G mediante resolución numérica de las ecuaciones de Maxwell.
⋆Diseño de antenas y arrays de antenas para 5G mediante resolución numérica de las ecuaciones de Maxwell.
⋆Sintonía asistida por ordenador de filtros y diplexores para 5G a partir de medidas.
⋆Caracterización y reducción de la sección radar de distintos objetos mediante resolución numérica de las ecuaciones de Maxwell.
⋆Estudio de fenómenos electromagnéticos singulares mediante resolución numérica de las ecuaciones de Maxwell.
Aviso a navegantes: estos proyectos exigen un gran esfuerzo y dedicación por parte del alumno y requieren un año de trabajo.
Introducción a las superficies minimales en el espacio euclídeo
Propuesta de TFG para alumnos de GIB o de GITST
Director:
Alberto Soria Marina, alberto.soria@upm.es
Descripción:
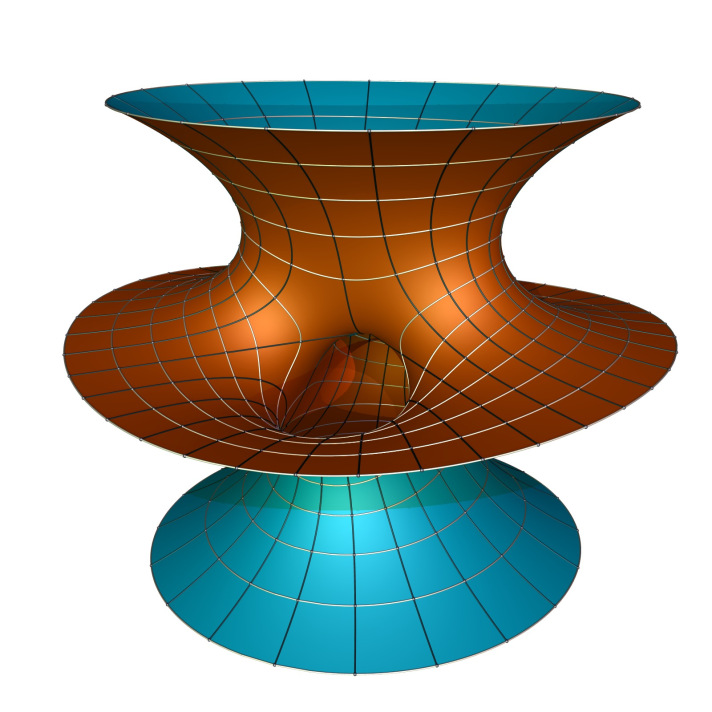
El principio de mínima acción de Maupertuis afirma que “en todo cambio que tiene lugar en la naturaleza, la cantidad de acción necesaria para que éste se produzca ha de ser la mínima posible”. Este principio se manifiesta asimismo en la geometría de ciertas superficies euclídeas denominadas minimales, que tienen la interesante propiedad de minimizar el área de todas aquellas superfices que comparten la misma curva cerrada de Jordan por frontera. Las superfices minimales son importantes en el mundo científico y aparecen con frecuencia en la naturaleza. La propuesta para este trabajo es el estudio y análisis de los fundamentos geométricos que permitan comprender la estructura matemática de dichas superfices.
Geometría de la relatividad especial
Propuesta de TFG para alumnos de GIB o de GITST
Director:
Alberto Soria Marina, alberto.soria@upm.es
Descripción:
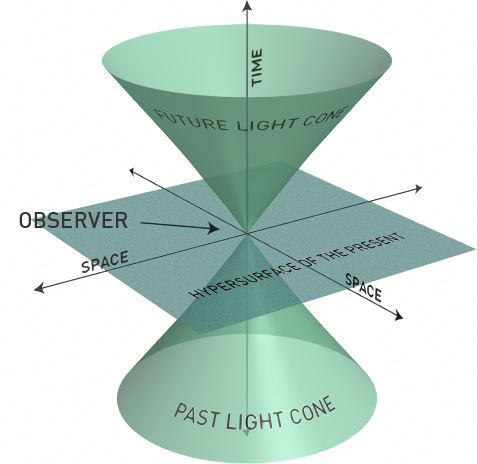
El espacio tiempo de Minkowski es una variedad Lorentziana 4-dimensional y con curvatura nula que sirve para modelar la teoría de la relatividad especial de Einstein, publicada en 1905. A pesar de guardar determinadas analogías con el espacio euclídeo, la signatura (1,3) de su tensor métrico hace que sus propiedades geométricas difieran de las euclídeas (por ejemplo existen vectores no nulos con longitudes nulas o negativas). La propuesta para este trabajo es introducir al alumno en la teoría de la relatividad especial de Einstein mediante el estudio de propiedades fundamentales del espacio-tiempo de Minkowski (simetría, causalidad, energía relativista, subvariedades, etc.) .
Generación de polinomios irreducibles sobre cuerpos finitos para la construcción de códigos detectores y correctores de errores
Director:
Lorenzo Martín García, lorenzojavier.martin@upm.es
Descripción:
La utilización de polinomios irreducibles sobre cuerpos finitos es fundamental para la construcción de códigos detectores y correctores de errores adaptados a las necesidades del usuario. Aunque hay criterios que permiten determinar si algún tipo de polinomios son irreducibles, no existe un criterio general que nos asegure que un polinomio de un determinado grado es irreducible. Se pretende abordar el problema a la inversa: a partir de unas condiciones genéricas sobre el polinomio: grado, cuerpo de los coeficientes, número de elementos no nulos, etc. construir un polinomio irreducible que cumpla esas condiciones o la mayoría de ellas.
Generación y evaluación de Tests Adaptativos Informatizados (TAI) para la evaluación académica
Director:
Lorenzo Martín García, lorenzojavier.martin@upm.es
Descripción:
Los tests adaptativos informatizados (TAI) permiten clasificar las facetas de la personalidad de un individuo sin necesidad de tener que responder a un test completo de personalidad ya que con un número reducido de preguntas -que se van proponiendo según las respuestas que se producen- es posible obtener los mismos resultados que si se pasara el bloque completo de preguntas. Sería interesante establecer estrategias que se concreten en programas informáticos que apliquen estas técnicas y comprobar -mediante experimentos específicos – en qué tipo de asignaturas pueden ser efectivas para la evaluación académica de los alumnos.
Grupo Simétrico y aplicación de la teoría de Galois a la resolución de ecuaciones polinómicas
Director:
Lorenzo Martín García, lorenzojavier.martin@upm.es
Descripción:
Desde el punto de vista teórico, la resolución de ecuaciones polinómicas es una aplicación clásica y elegante de la teoría de Galois en la que juega un papel importante el Grupo Simétrico de las permutaciones de los elementos de un conjunto finito. Hay muchos programas informáticos que resuelven ecuaciones polinómicas de manera eficiente. En este caso, se busca un programa que resuelva las ecuaciones polinómicas de tercer y cuarto grado aplicando las ecuaciones resolventes que proporciona la teoría de Galois y que ilustre el comportamiento del grupo simétrico y de sus subgrupos más importantes.
