Integral indefinida

Dada una función f definida en un intervalo I se dice que otra función F es una primitiva de f en I si  F es derivable en I y F'=f en I.

Si consideramos la función f(x)=2x, las funciones

son primitivas de f pues la derivada de cada una de ellas es 2x.

Dada una función f, no existe para ella una única primitiva F, ya que cualquier otra función de la forma F+C, donde C es una constante, también cumple la condición de que su derivada es igual a f

Además, si F y G son primitivas de f en I entonces F-G=C (constante) en I pues

Las primitivas de una función forman una familia de funciones cuya representación gráfica es siempre la misma, estando cada una desplazada verticalmente respecto de las demás:

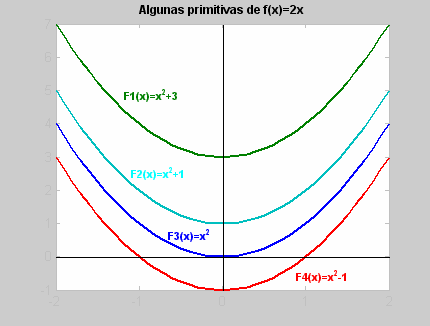
Al conjunto de todas las primitivas de una función  f se le llama integral indefinida de f y se representa por

Para f(x)=2x se tiene

Teniendo en cuenta  las derivadas de las funciones f  "elementales" (potencias, exponenciales, trigonométricas, y sus inversas) obtenemos las siguiente integrales indefinidas:

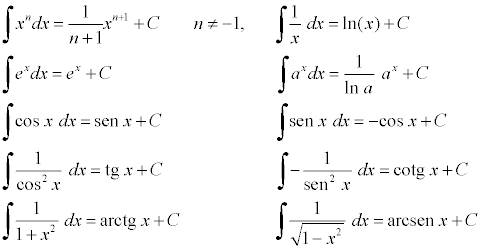
Las igualdades anteriores son ciertas cuando las expresiones que aparecen en ellas tienen sentido. Así, por ejemplo

Para f(x)=1/x  en I=(0,+∞) tenemos

Sin embargo en  I=(- ∞,0) obtenemos

Propiedades de la integral indefinida

Se verifica:

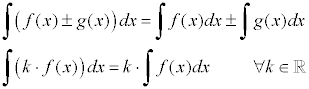
Estas propiedades son consecuencia de la linealidad de la derivación:

Utilizando la propiedad de linealidad de la integral indefinida y las primitivas de funciones sencillas podemos calcular la siguiente integral:

La generalización de estos resultados aparece en la tabla de integración inmediata.