Optimización multicriterio para el entrenamiento y explicabilidad de máquinas basadas en aprendizaje automático

Director:
Pedro J. Zufiria Zatarain. Despacho: (A-306). Email: pedro.zufiria@upm.es

Descripción:
En el TFM abordaremos el diseño y la evaluación de modelos/máquinas de aprendizaje automático, que se emplean fundamentalmente en el ámbito de la Inteligencia Artificial. Las formulaciones multicriterio nos permitirán, por un lado, diseñar máquinas más robustas empleando técnicas de optimización bayesiana. Por otro lado, también emplearemos esas formulaciones para explicar el comportamiento y algunas propiedades  de las máquinas que diseñemos.
Para realizar el TFM, se requiere que el alumno tenga (o adquiera) formación en optimización de funciones, modelado probabilístico e inferencia estadística. Por otro lado, aunque no es imprescindible, se valorará que el alumno tenga soltura programando algoritmos (o empleando los ya existentes).

Criptografía en la Blockchain

Criptografía en la Blockchain

Director:
Vicente Jara Vera. Despacho: (A-315). Email: vicente.jara@upm.es

Descripción:
La cadena de bloques (blockchain) es una tecnología de almacenamiento de información que tiene entre sus fundamentos la criptografía.
Se ofertan TFGs y TFMs relativos a la criptografía utilizada en las diferentes blockchain y sus diversos escenarios.
Se pretende que se conozca el funcionamiento general de la blockchain, su estructura, tipología y características, así como los diversos modos de consenso entre nodos.
Se incidirá a partir de los anterior en los aspectos matemáticos criptográficos propios de la cadena de bloques: criptografía simétrica, asimétrica y firmas digitales, funciones hash, o pruebas de conocimiento-cero, entre las principales.

Métodos criptoanalíticos

Director:
Vicente Jara Vera. Despacho: (A-315). Email: vicente.jara@upm.es

Descripción:
El criptoanálisis es la disciplina cuyo objeto es la obtención de la información (parcial o total) de un mensaje cifrado sin concurso de la clave de descifrado.
Se ofertan TFGs y TFMs relativos a los diversos métodos criptoanalíticos (sobre sistemas de cifrado clásicos o modernos).
Entre ellos: las máquinas de rotores, para los sistemas clásicos; el ataque lineal, diferencial, de particiones, etc., para los cifrados simétricos; algoritmos de factorización generales y específicos, entre ellos las diversas cribas, para la criptografía basada en la factorización de enteros; ataques al problema del logaritmo discreto; ataques a la criptografía de curva elíptica; algoritmos cuánticos, como el de Peter Shor, etc.

Comparativa de métodos de reducción de dimensionalidad y clustering para el análisis de electroneurogramas

Oferta de TFG para alumnos de GIB

Directores:
Francisco José Navarro Valero, ETSIT-UPM. Despacho: A302-4. E-mail: francisco.navarro@upm.es
Amparo Güemes González, Department of Engineering, University of Cambridge, UK

Descripción:
El TFG consitirá en hacer una comparativa de métodos de reducción de dimensionalidad (PCA, t-SNE, UMAP…) y clustering en señales nerviosas (electroneurogramas) obtenidas por electrodos colocados en nervios periféricos. El procesamiento de estas señales eléctricas incluye varios pasos. Primero se deben preprocesar (ej. filtrado y eliminación de artefactos), después de detectan los eventos de interés (compound action potentials ‘CAP’ o potenciales de acción compuestos) aplicando un umbral que puede ser fijo o adaptativo. Una vez se extraen los picos detectados (‘waveforms’), lo interesante es aplicar clustering para agruparlos en tipos según su forma, pero antes de ello es necesario reducir la alta dimensionalidad de estas waveforms, para lo cual existen distintos métodos (PCA, t-SNE, UMAP…). Realizar un estudio sobre el impacto de la elección de los métodos de reducción de dimensionalidad y clustering, y de sus parámetros en la identificación de tipos de señales es muy importante para entender el origen fisiológico de las mismas.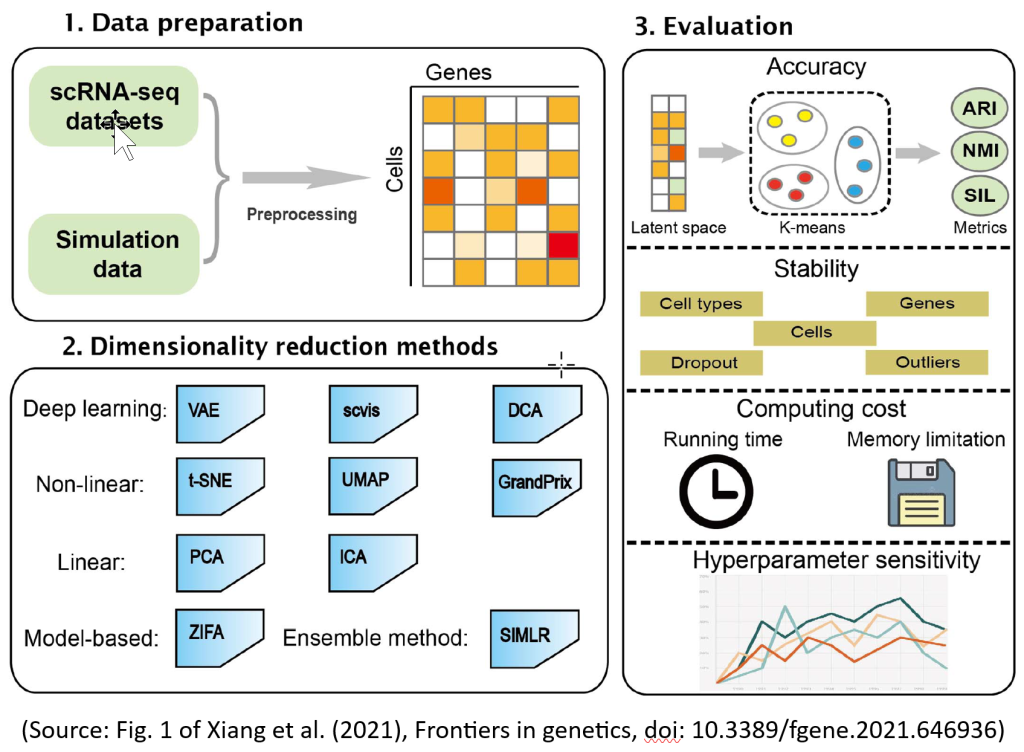

Electromagnetismo computacional

Director:
Valentín de la Rubia Hernández. Despacho: A-313. E-mail: valentin.delarubia@upm.es

Descripción:
Se oferta una serie de proyectos dentro de la línea de investigación de electromagnetismo computacional. Estos proyectos tienen como denominador común la resolución de la ecuaciones de Maxwell de forma eficiente mediante ordenador con el objetivo de realizar diseños de distintos dispositivos electromagnéticos que aparecen en todo sistema de telecomunicación, como por ejemplo filtros, diplexores, triplexores, antenas y array de antenas en las bandas de microondas y milimétricas.
⋆Desarrollo e implementación de métodos numéricos en electromagnetismo.
⋆Diseño de filtros y diplexores para 5G mediante resolución numérica de las ecuaciones de Maxwell.
⋆Diseño de antenas y arrays de antenas para 5G mediante resolución numérica de las ecuaciones de Maxwell.
⋆Sintonía asistida por ordenador de filtros y diplexores para 5G a partir de medidas.
⋆Caracterización y reducción de la sección radar de distintos objetos mediante resolución numérica de las ecuaciones de Maxwell.
⋆Estudio de fenómenos electromagnéticos singulares mediante resolución numérica de las ecuaciones de Maxwell.

Aviso a navegantes: estos proyectos exigen un gran esfuerzo y dedicación por parte del alumno y requieren un año de trabajo.

Propiedades geométricas de curvas y superficies en R² y R³

Propuesta de TFG para alumnos de GITST, GIB o GISD

Director:
Alberto Soria Marina. Despacho: A-311. E-mail: alberto.soria@upm.es
ETSI Telecomunicación, UPM. Dpto. Matemática Aplicada a las TIC 

Descripción: 
Las curvas y superficies euclídeas son variedades topológicas que aparte de tener un gran interés matemático, presentan también numerosas aplicaciones en el ámbito de la física y la ingeniería. La propuesta para este trabajo es realizar un estudio de elementos relevantes asociados a estas variedades en función de los intereses del alumno. Entre ellos figuran la curvatura y torsión de una curva, la curvatura normal, media, y de Gauss en una superficie, las líneas asintóticas y de curvatura, las curvas geodésicas, etc. De igual forma, podrían ser objeto de estudio determinadas familias de curvas y superficies notables, como las de Bézier, las superficies minimales, de curvatura media constante, con curvatura de Gauss constante, regladas, etc. Este análisis se complementará con el uso de programas informáticos que faciliten los cálculos y las representaciones gráficas.

Geometría de la relatividad especial

Propuesta de TFG para alumnos de GITST, GIB o GISD

Director:
Alberto Soria Marina. Despacho: A-311. E-mail: alberto.soria@upm.es
ETSI Telecomunicación, UPM. Dpto. Matemática Aplicada a las TIC

Descripción:
El espacio tiempo de Minkowski es una variedad lorentziana 4-dimensional y con curvatura nula que sirve para modelar la teoría de la relatividad especial de Einstein, publicada en 1905. A pesar de guardar determinadas analogías con el espacio euclídeo, la signatura (1,3) de su tensor métrico hace que sus propiedades geométricas difieran de las euclídeas (por ejemplo, existen vectores no nulos con longitudes nulas o negativas). La propuesta para este trabajo es introducir al alumno en la teoría de la relatividad especial de Einstein mediante el estudio de propiedades fundamentales del espacio-tiempo de Minkowski (simetría, causalidad, electrodinámica relativista, subvariedades, etc.). 

Generación de polinomios irreducibles sobre cuerpos finitos para la construcción de códigos detectores y correctores de errores

Director:
Lorenzo Martín García. Despacho: A-307. Email: lorenzojavier.martin@upm.es

Descripción:

La utilización de polinomios irreducibles sobre cuerpos finitos es fundamental para la construcción de códigos detectores y correctores de errores adaptados a las necesidades del usuario. Aunque hay criterios que permiten determinar si algún tipo de polinomios son irreducibles, no existe un criterio general que nos asegure que un polinomio de un determinado grado es irreducible. Se pretende abordar el problema a la inversa: a partir de unas condiciones genéricas sobre el polinomio: grado, cuerpo de los coeficientes, número de elementos no nulos, etc. construir un polinomio irreducible que cumpla esas condiciones o la mayoría de ellas.

Generación y evaluación de Tests Adaptativos Informatizados (TAI) para la evaluación académica

Director:
Lorenzo Martín García. Despacho: A-307. Email: lorenzojavier.martin@upm.es

Descripción:

Los tests adaptativos informatizados (TAI) permiten clasificar las facetas de la personalidad de un individuo sin necesidad de tener que responder a un test completo de personalidad ya que con un número reducido de preguntas -que se van proponiendo según las respuestas que se producen- es posible obtener los mismos resultados que si se pasara el bloque completo de preguntas. Sería interesante establecer estrategias que se concreten en programas informáticos que apliquen estas técnicas y comprobar -mediante experimentos específicos – en qué tipo de asignaturas pueden ser efectivas para la evaluación académica de los alumnos.

Grupo Simétrico y aplicación de la teoría de Galois a la resolución de ecuaciones polinómicas

Director:
Lorenzo Martín García. Despacho: A-307. Email: lorenzojavier.martin@upm.es

Descripción:

Desde el punto de vista teórico, la resolución de ecuaciones polinómicas es una aplicación clásica y elegante de la teoría de Galois en la que juega un papel importante el Grupo Simétrico de las permutaciones de los elementos de un conjunto finito. Hay muchos programas informáticos que resuelven ecuaciones polinómicas de manera eficiente. En este caso, se busca un programa que resuelva las ecuaciones polinómicas de tercer y cuarto grado aplicando las ecuaciones resolventes que proporciona la teoría de Galois y que ilustre el comportamiento del grupo simétrico y de sus subgrupos más importantes.